A B. 4852. feladat (2017. február)

B. 4852. Az $\displaystyle ABC$ háromszögbe és a háromszög köré az ábra szerint írtuk az $\displaystyle A_1B_1C_1$ és $\displaystyle A_2B_2C_2$ háromszögeket, ahol $\displaystyle A_1B_1\parallel A_2B_2$, $\displaystyle B_1C_1\parallel B_2C_2$ és $\displaystyle C_1A_1\parallel C_2A_2$ is teljesül. Az $\displaystyle ABC$, $\displaystyle A_1B_1C_1$ és $\displaystyle A_2B_2C_2$ háromszögek területei rendre $\displaystyle t$, $\displaystyle t_1$ és $\displaystyle t_2$.

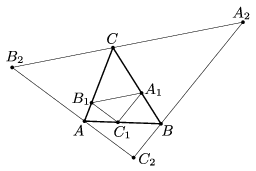
Bizonyítsuk be, hogy $\displaystyle t^2=t_1\cdot t_2$.

Javasolta: Róka Sándor (Nyíregyháza)

(5 pont)

A beküldési határidő 2017. március 10-én LEJÁRT.

Megoldás. A $\displaystyle C, C_{1}, C_{2}$ csúcsokkal szemközti oldalak (a szokásos jelölések szerint) $\displaystyle c, c_{1}, c_{2}$, a hozzájuk tartozó magasságok rendre $\displaystyle m, m_{1}, m_{2}$.

Az $\displaystyle A_{1}B_{1}C_{1}$ és $\displaystyle A_{2}B_{2}C_{2}$ háromszögek hasonlóak, tehát $\displaystyle \frac{c_{1}}{c_{2}}=\frac{m_{1}}{m_{2}}$, azaz $\displaystyle c_{1}\cdot m_{2}=c_{2}\cdot m_{1}$. Emiatt

$\displaystyle t_{1}\cdot t_{2}=\Big {(}\frac{1}{2}c_{1}\cdot m_{1}\Big{)}\Big {(}\frac{1}{2}c_{2}\cdot m_{2}\Big{)}=\frac{1}{4}c_{1}\cdot m_{1}\cdot c_{2}\cdot m_{2}=\frac{1}{4}\Big {(}c_{1}\cdot m_{2}\Big{)}^{2}.$

Mivel $\displaystyle B_{1}C_{1}\| AC_{2}$ ezért a $\displaystyle B_{1}C_{1}A$ és $\displaystyle B_{1}C_{1}C_{2}$ háromszögeknek egy-egy oldala és a hozzájuk tartozó magasság megegyezik, tehát egyenlő a területük. Hasonlóan $\displaystyle C_{1}A_{1} \| C_{2}B$ és azonnal adódik, hogy szintén megegyezik a $\displaystyle C_{1}A_{1}B$ és $\displaystyle C_{1}A_{1}C_{2}$ háromszögek területe is.

Az $\displaystyle ABC$ háromszög területe egyenlő a $\displaystyle CB_{1}C_{2}A_{1}$ négyszög területével, mivel a $\displaystyle CB_{1}C_{1}A_{1}$ négyszöget mindkét síkidom tartalmazza, továbbá beláttuk, hogy a $\displaystyle B_{1}C_{1}A$ és $\displaystyle B_{1}C_{1}C_{2}$, illetve a $\displaystyle C_{1}A_{1}B$ és $\displaystyle C_{1}A_{1}C_{2}$ háromszögek területe is megegyezik.

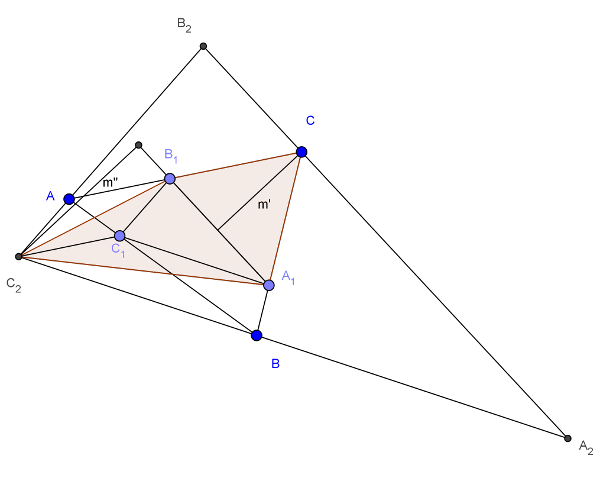
A $\displaystyle CB_{1}C_{2}A_{1}$ négyszög az $\displaystyle A_{1}B_{1}$ átlóval két háromszögre bontható, így területe az ábra jelöléseivel $\displaystyle t=\frac{1}{2}c_{1}(m'+m'')$. Mivel $\displaystyle m'+m''=m_{2}$, ezért $\displaystyle t=\frac{1}{2}c_{1}m_{2}$, amiből $\displaystyle t^2==\frac{1}{4}\Big {(}c_{1}\cdot m_{2}\Big{)}^{2}$.

Ezzel igazoltuk, hogy $\displaystyle t^{2}=t_{1}\cdot t_{2}$.

Statisztika:

62 dolgozat érkezett.
5 pontot kapott:	Al-Sayyed Zakariás, Andó Angelika, Ardai István Tamás, Baran Zsuzsanna, Borbényi Márton, Busa 423 Máté, Csahók Tímea, Csiszár Zoltán, Csuha Boglárka, Daróczi Sándor, Döbröntei Dávid Bence, Fekete Balázs Attila, Fülöp Anna Tácia, Gáspár Attila, Győrffy Ágoston, György Levente, Horváth Péter, Imolay András, Kerekes Anna, Kocsis Júlia, Kovács 246 Benedek, Kovács 654 Áron , Kővári Péter Viktor, Lakatos Ádám, Mészáros Anna, Mikulás Zsófia, Nagy Nándor, Olosz Adél, Pap Benedek, Richlik Róbert, Schrettner Jakab, Simon Dániel Gábor, Szabó 417 Dávid, Szabó Kristóf, Tiderenczl Dániel, Tóth Viktor, Török Zsombor Áron, Várkonyi Dorka, Velkey Vince, Weisz Máté.
4 pontot kapott:	13 versenyző.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2017. februári matematika feladatai