 Problem B. 4868. (April 2017)
Problem B. 4868. (April 2017)
B. 4868. In a triangle \(\displaystyle ABC\), \(\displaystyle AC<AB\) and the median \(\displaystyle AF\) divides the angle at \(\displaystyle A\) in a \(\displaystyle 1:2\) ratio. The perpendicular drawn to \(\displaystyle AB\) at \(\displaystyle B\) intersects line \(\displaystyle AF\) at \(\displaystyle D\). Show that \(\displaystyle AD=2AC\).
(3 pont)
Deadline expired on May 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
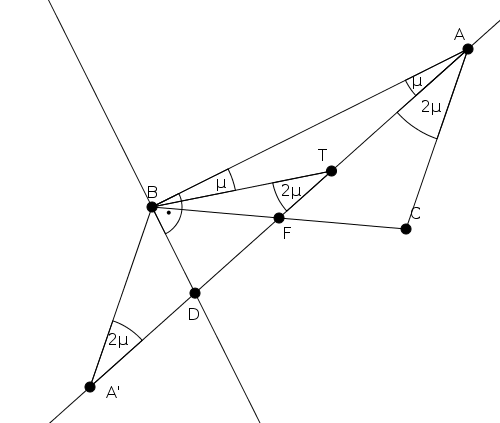
Megoldásvázlat. Legyen \(\displaystyle A\) tükörképe \(\displaystyle F\)-re \(\displaystyle A'\), \(\displaystyle AD\) felezéspontja \(\displaystyle T\), \(\displaystyle FAB\angle=\mu\), s így \(\displaystyle FAC\angle=2\mu\). Mivel \(\displaystyle T\) a \(\displaystyle BDA\) derékszögű háromszög Thalész-körének középpontja, így \(\displaystyle BAT\triangle\) egyenlőszárú, \(\displaystyle TBA\angle=\mu\), amiért \(\displaystyle BTA'\angle=2\mu\). A tükrözés miatt \(\displaystyle BA'T\angle=2\mu\), ezért \(\displaystyle BA'T\triangle\) egyenlőszárú, \(\displaystyle A'B=BT\). Ismét a tükrözés, illetve a Thalész-tétel miatt \(\displaystyle AC=A'B=BT=AD/2\).
Statistics:
53 students sent a solution. 3 points: Beke Csongor, Besenyi Tibor, Csiszár Zoltán, Csuha Boglárka, Deák Bence, Döbröntei Dávid Bence, Dömsödi Bálint, Fekete Balázs Attila, Fülöp Anna Tácia, Füredi Erik Benjámin, Garamvölgyi István Attila, Geretovszky Anna, Győrffy Ágoston, Horváth Péter, Jánosik Áron, Kerekes Anna, Kiss Roberta Zsófia, Kocsis Júlia, Kőrösi Ákos, Lajkó Áron, Lakatos Ádám, Lukács Lilla Réka, Márton Dénes, Mikulás Zsófia, Noszály Áron, Olosz Adél, Páli Petra, Paulovics Péter, Póta Balázs, Richlik Róbert, Saár Patrik, Sáfi Lilla, Scheidler Barnabás, Simon Dániel Gábor, Szabó 417 Dávid, Szécsényi Nándor, Szemerédi Levente, Szepesi Zoltán, Tanács Viktória, Tiderenczl Dániel, Tóth 111 Máté , Tran 444 Ádám, Vári-Kakas Andor, Várkonyi Dorka, Varsányi András, Williams Hajna, Zólomy Kristóf, Zsigri Bálint. 2 points: Török Ádám. 1 point: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, April 2017
