 |
A B. 4889. feladat (2017. szeptember) |
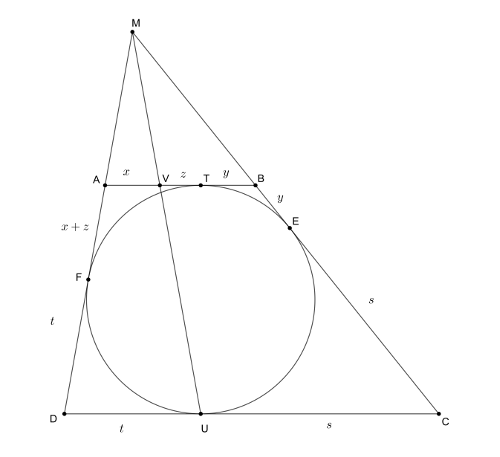
B. 4889. Az \(\displaystyle ABCD\) érintőtrapéz beírt köre az \(\displaystyle AB\) alapot a \(\displaystyle T\), a vele párhuzamos \(\displaystyle CD\) alapot az \(\displaystyle U\) pontban érinti. Legyen \(\displaystyle M\) az \(\displaystyle AD\) és \(\displaystyle BC\) száregyenesek metszéspontja, és legyen \(\displaystyle V\) az \(\displaystyle AB\) oldal és az \(\displaystyle MU\) egyenesek metszéspontja. Mutassuk meg, hogy \(\displaystyle AT=VB\).
(4 pont)
A beküldési határidő 2017. október 10-én LEJÁRT.
Megoldásvázlat. Legyen \(\displaystyle AV=x\), \(\displaystyle VT=z\), \(\displaystyle TB=BE=y\), \(\displaystyle FD=DU=t\), \(\displaystyle UC=CE=s\), \(\displaystyle AF=AT=x+z\). A beírt kör átmérőjének négyzete Pitagorasz tétele szerint \(\displaystyle (x+z+t)^2 - (x+z-t)^2 = (s+y)^2 - (s-y)^2\), amiből \(\displaystyle \dfrac{x+z}{s}=\dfrac{y}{t}\). A párhuzamos szelők tételéből pedig \(\displaystyle \dfrac{x}{t}=\dfrac{y+z}{s}\). E két utóbbi egyenlőséget összeszorozva: \(\displaystyle \dfrac{x(x+z)}{st}=\dfrac{y(y+z)}{st}\), \(\displaystyle x^2-y^2 + z(x-y)=0\), \(\displaystyle (x-y)(x+y+z)=0\), azaz \(\displaystyle x=y\), így \(\displaystyle AT=x+z= y+z= VB\).
Statisztika:
90 dolgozat érkezett. 4 pontot kapott: 57 versenyző. 3 pontot kapott: 21 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 7 versenyző.
A KöMaL 2017. szeptemberi matematika feladatai

