A B. 4910. feladat (2017. november)

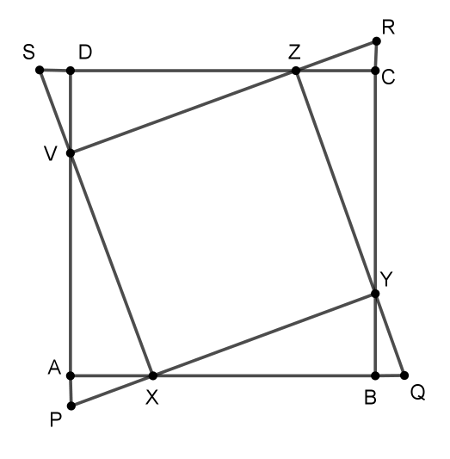
B. 4910. Az $\displaystyle ABCD$ négyzet oldalegyenesein vegyük fel a $\displaystyle P$, $\displaystyle Q$, $\displaystyle R$ és $\displaystyle S$ pontokat az ábra szerint úgy, hogy $\displaystyle AP=BQ=CR=DS$. Az $\displaystyle AB$ oldal tetszőleges belső $\displaystyle X$ pontjából kiindulva a $\displaystyle PX$ egyenes messe $\displaystyle BC$ egyenesét $\displaystyle Y$-ban, $\displaystyle QY$ messe $\displaystyle CD$ egyenesét $\displaystyle Z$-ben, $\displaystyle RZ$ a $\displaystyle DA$ egyenest $\displaystyle V$-ben, végül $\displaystyle SV$ az $\displaystyle AB$ egyenest $\displaystyle X'$-ben. Bizonyítsuk be hogy ha $\displaystyle X'$ és $\displaystyle X$ egybeesnek, akkor $\displaystyle XYZV$ négyzet.

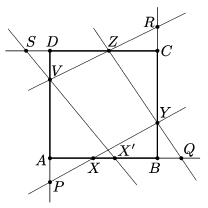
(5 pont)

A beküldési határidő 2017. december 11-én LEJÁRT.

Megoldás. Legyen a négyzet oldala egységnyi és $\displaystyle AP=BQ=CR=DS=s$, $\displaystyle AX=t$ és $\displaystyle BY=f(t)$.

Ekkor $\displaystyle PAX$ és $\displaystyle YBX$ egymáshoz hasonló derékszögű háromszögek, hiszen $\displaystyle AXP\sphericalangle = BXY\sphericalangle$ hegyesszögeik csúcsszögek. Így $\displaystyle AX:AP=XB:YB$, azaz $\displaystyle \dfrac{t}{s}=\dfrac{1-t}{f(t)}$ szerint $\displaystyle f(t)=s\dfrac{1-t}{t}=\dfrac{s}{t}-s$. Ugyanígy

$\displaystyle CZ=f(BY)=f(f(t))=\dfrac{s}{\dfrac{s}{t}-s}-s=\dfrac{1}{\dfrac{1}{t}-1}-s= \dfrac{t}{1-t}-s=-(s+1)+\dfrac{1}{1-t},$

$\displaystyle AX'=f(DV)=f(f(CZ))=-(s+1)+\dfrac{1}{1-CZ}= -(s+1)+\dfrac{1}{1-\left(-(s+1)+\dfrac{1}{1-t}\right)}=$

$\displaystyle =-(s+1)+\dfrac{1-t}{1-t-t+s(1-t)}=-(s+1)+\dfrac{1-t}{(s+1)-(s+2)t}.$

Ha $\displaystyle X'$ és $\displaystyle X$ egybeesnek, akkor $\displaystyle AX'=AX$, azaz $\displaystyle -(s+1)+\dfrac{1-t}{(s+1)-(s+2)t}=t$. Ez $\displaystyle t$-ben másodfokú egyenletre vezet:

$\displaystyle -(s+1)((s+1)-(s+2)t)+(1-t)=t((s+1)-(s+2)t),$

$\displaystyle (s+2)t^2 + (s^2+2s)t -(s^2+2s) =0,$

$\displaystyle (s+2)(t^2 + st -s)=0.$

Mivel $\displaystyle s>0$, azért az egyenlet egyetlen pozitív megoldása $\displaystyle t_1=\dfrac{-s+\sqrt{s^2+4s}}{2}$. Ezzel

$\displaystyle BY=f(t_1)=\dfrac{s}{t_1}-s=\dfrac{2s}{-s+\sqrt{s^2+4s}}-s= \dfrac{2s(s+\sqrt{s^2+4s})}{4s}-s=t_1,$

vagyis $\displaystyle BY=f(AX)=AX$, ugyanígy $\displaystyle CZ=f(BY)=BY$, $\displaystyle DV=f(CZ)=CZ$ és $\displaystyle AX=AX'=f(DV)=DV$. Ebből következik, hogy az $\displaystyle ABCD$ négyzet középpontja körüli 90 fokos elforgatás az egész alakzatot, így az $\displaystyle XYZV$ négyszöget is önmagára képezi, tehát $\displaystyle XYZV$ valóban négyzet.

Statisztika:

69 dolgozat érkezett.
5 pontot kapott:	Beke Csongor, Busa 423 Máté, Csépányi István, Csizmadia Viktória, Daróczi Sándor, Deák Bence, Dobák Dániel, Döbröntei Dávid Bence, Fekete Richárd, Fülöp Anna Tácia, Füredi Erik Benjámin, Gáspár Attila, Gyetvai Miklós, Hervay Bence, Jánosik Áron, Janzer Orsolya Lili, Jedlovszky Pál, Kerekes Anna, Kószó Máté József, Lukács Lilla Réka, Márton Dénes, Molnár-Sáska Zoltán, Nagy Nándor, Noszály Áron, Pituk Gábor, Póta Balázs, Saár Patrik, Schifferer András, Schrettner Jakab, Shuborno Das, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Szabó 997 Balázs István, Tiderenczl Dániel, Tiszay Ádám, Tubak Dániel, Vári-Kakas Andor, Várkonyi Zsombor, Velkey Vince, Weisz Máté, Zólomy Kristóf, Zsigri Bálint.
4 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	13 versenyző.

A KöMaL 2017. novemberi matematika feladatai