 |
A B. 4929. feladat (2018. január) |
B. 4929. Adott az \(\displaystyle \mathcal E\) ellipszis és a \(\displaystyle \mathcal H\) hiperbola a térben úgy, hogy síkjaik merőlegesek egymásra, valamint \(\displaystyle \mathcal E\) fókuszai \(\displaystyle \mathcal H\) valós tengelyének végpontjai, \(\displaystyle \mathcal H\) fókuszai pedig \(\displaystyle \mathcal E\) nagytengelyének végpontjai. Legyen \(\displaystyle A\) és \(\displaystyle B\) két rögzített pont a \(\displaystyle \mathcal H\) hiperbola különböző ágain, továbbá \(\displaystyle P\) legyen az ellipszis egy tetszőleges pontja. Mutassuk meg, hogy a \(\displaystyle PA+PB\) távolságösszeg nem függ \(\displaystyle P\) megválasztásától.
(6 pont)
A beküldési határidő 2018. február 12-én LEJÁRT.
1. megoldás. A megoldáshoz fel fogunk használni több jól ismert, a kúpszeletekre vonatkozó tényt, amelyeket meg lehet találni például a http://mathworld.wolfram.com/Ellipse.html és http://mathworld.wolfram.com/Hyperbola.html, vagy a https://en.wikipedia.org/wiki/Conic_section oldalakon.
Vegyük fel a derékszögű koordinátarendszert úgy, hogy \(\displaystyle \mathcal{E}\) nagytengelye az \(\displaystyle x\)-, kistengelye az \(\displaystyle y\)-tengelyen legyen, \(\displaystyle \mathcal{H}\) valós tengelye az \(\displaystyle x\)-, képzetes tengelye pedig a \(\displaystyle z\)-tengely legyen.
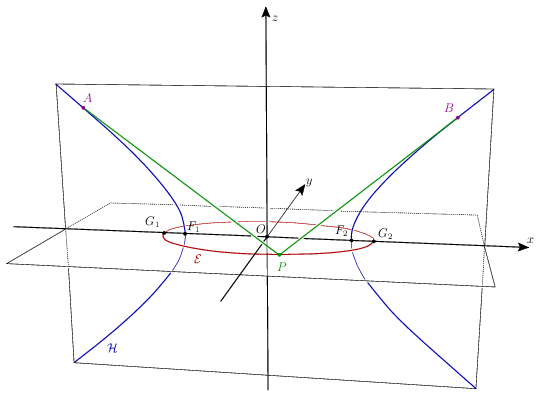
Az \(\displaystyle \mathcal{E}\) fókuszpontjai legyenek \(\displaystyle F_1=(-f,0,0)\) és \(\displaystyle F_2=(f,0,0)\), a nagytengelyének végpontjai \(\displaystyle G_1=(-a,0,0)\) és \(\displaystyle G_2=(a,0,0)\). A kistengely végpontjai \(\displaystyle (0,b,0)\) és \(\displaystyle (0,-b,0)\). Mint ismeretes, az \(\displaystyle a,b\) féltengelyekre és az \(\displaystyle f\) lineáris excentricitásra (a fókuszpontoknak a középponttól való távolságára) teljesül, hogy
\(\displaystyle a^2=b^2+f^2. \)
Azt, hogy a \(\displaystyle P\) pont rajta van \(\displaystyle \mathcal{E}\)-n, az ellipszis paraméteres egyenletével írjuk fel: alkalmas \(\displaystyle t\) valós számmal
\(\displaystyle P = (a\cos t, b\sin t, 0). \)
A \(\displaystyle \mathcal{H}\) fókuszpontjai \(\displaystyle G_1\) és \(\displaystyle G_2\), valós tengelyének végpontjai \(\displaystyle F_1\) és \(\displaystyle F_2\), tehát a lineáris excentricitása \(\displaystyle a\), a fél valóstengely hossza \(\displaystyle f\). A képzetes fél tengely hossza éppen \(\displaystyle \sqrt{a^2-f^2}=b\).
Feltehetjük, hogy az \(\displaystyle A\) pont az \(\displaystyle x<0\) féltérben, az \(\displaystyle B\) pont az \(\displaystyle x>0\) féltérben van. A hiperbola paraméteres egyenlete szerint alkalmas \(\displaystyle u,v\) valós számokkal
\(\displaystyle A=(-f\ch u, 0, b\sh u), \quad B=(f\ch v, 0, b\sh v). \)
Ezek után kifejezhetjük a \(\displaystyle PA\) és \(\displaystyle PB\) távolságokat az \(\displaystyle a,b,u,v,t\) számokkal:
\(\displaystyle PA^2 = (a\cos t-f\ch u)^2 + (b\sin t)^2 + (b\sh u)^2 = \)
\(\displaystyle = (a\cos t-f\ch u)^2 +b^2(1-\cos^2t)+b^2(\ch^2u-1) = \)
\(\displaystyle = (a^2-b^2)\cos^2t -2af\cos t\ch u+(f^2+b^2)\ch^2u = \)
\(\displaystyle = f^2\cos^2t -2af\cos t\ch u+a^2\ch^2u = (a\ch u-f\cos t)^2. \)
Az utolsó zárójelben pozitív szám áll, mert \(\displaystyle a>f\) és \(\displaystyle \ch u\ge1\ge\cos t\). Így tehát
\(\displaystyle PA = a\ch u-f\cos t. \)
Hasonlóan,
\(\displaystyle PB^2 = (a\cos t+f\ch v)^2 + (b\sin t)^2 + (b\sh v)^2 = \)
\(\displaystyle = (a\cos t+f\ch v)^2 +b^2(1-\cos^2t)+b^2(\ch^2v-1) = \)
\(\displaystyle = (a^2-b^2)\cos^2t +2af\cos t\ch v+(f^2+b^2)\ch^2v = \)
\(\displaystyle = f^2\cos^2t +2af\cos t\ch v+a^2\ch^2v = (a\ch v+f\cos t)^2, \)
és
\(\displaystyle PB = a\ch v+f\cos t. \)
Ezzel azt akptuk, hogy
\(\displaystyle PA+PB = a\ch u+a\ch v, \)
ami nem függ a \(\displaystyle t\) paramétertől, vagyis a \(\displaystyle P\) megválasztásától.
2. megoldás. Továbbra is használjuk az 1. megoldás jelöléseit, és feltételezzük, hogy az \(\displaystyle A\) pont az \(\displaystyle G_1\)-hez közelebbi, a \(\displaystyle B\) pont pedig az \(\displaystyle G_2\) fókuszponthoz közelebbi hiperbolaágon van.
Megmutatjuk, hogy vannak olyan \(\displaystyle A\) és \(\displaystyle B\) csúcsú körkúpok, amelyek illeszkednek az \(\displaystyle \mathcal{E}\) ellipszisre. Ezekhez a kúpokhoz és az \(\displaystyle x-y\) síkhoz tartozó Dandelin-gömböket fogjuk rekonstruálni.
Az \(\displaystyle x-z\) síkban rajzoljuk meg az \(\displaystyle AG_1G_2\) háromszög beírt körét és a \(\displaystyle G_1G_2\) oldalhoz hozzáírt körét. Ezek érintsék az \(\displaystyle AG_1\), \(\displaystyle AG_2\) és \(\displaystyle G_1G_2\) egyeneseket a \(\displaystyle T_1,T_2,U_1,U_2,E_1,E_2\) pontokban az ábra szerint.
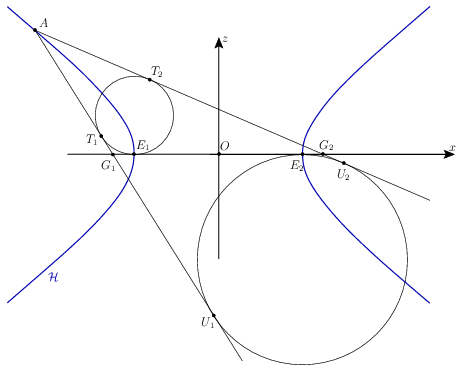
Az \(\displaystyle A,G_1,G_2\) pontokból a körökhöz húzott érintőszakaszok egyenlőségéből láthatjuk, hogy \(\displaystyle E_1G_2-E_1G_1=T_2G_2-T_1G_1=(AT_2+T_2G_2)-(AT_1+T_1G_1)=AG_2-AG_1\); viszont, mivel \(\displaystyle A\) és \(\displaystyle F_1\) is az a \(\displaystyle G_1\)-hez közelebbi hiperbolágon van, \(\displaystyle AG_2-AG_1=F_1G_2-F_1G_1\). Tehát \(\displaystyle E_1\) és \(\displaystyle F_1\) olyan pontok a \(\displaystyle G_1G_2\) szakaszon, amelyekre \(\displaystyle E_1G_1-E_1G_2=F_1G_2-F_1G_1\), amiből következik, hogy \(\displaystyle E_1=F_1\).
Hasonlóan, abból, hogy \(\displaystyle E_2G_1-E_2G_2=U_1G_1-U_2G_2=(AU_2-AG_2)-(AU_1-AG_1)=AG_2-AG_1= F_2G_1-F_2G_2\), láthatjuk, hogy \(\displaystyle E_2=F_2\).
Ezek után vegyük fel azt a \(\displaystyle \mathcal{D}_1\) gömböt, amelynek főköre az \(\displaystyle AG_1G_2\) háromszög beírt köre, és azt a \(\displaystyle \mathcal{D}_1'\) gömböt, amelynek főköre a hozzáírt kör. A két gömböt egymásba nagyíthatjuk az \(\displaystyle A\) pontból, tehát létezik egy olyan \(\displaystyle A\) csúcsú kúp, amely érinti mindkét gömböt. Az \(\displaystyle x-y\) sík mindkét gömböt érinti úgy, hogy a gömbök ellentétes oldalon vannak, tehát a kúp és az \(\displaystyle x-y\) sík metszete valamilyen ellipszis. Az ellipszis fókuszai az \(\displaystyle x-y\) sík érintési pontjai a két gömbön, tehát \(\displaystyle F_1\) és \(\displaystyle F_2\). A \(\displaystyle G_1\) és a \(\displaystyle G_2\) pont rajta van a metszeten. Az ellipszist egyértelműen meghatározza a két fókuszpont és egy pontja, ezért a metszet csak \(\displaystyle \mathcal{E}\) lehet.
Hasonlóan konstruálhatjuk meg a \(\displaystyle B\) ponthoz tartozó \(\displaystyle \mathcal{D}_2\) és \(\displaystyle \mathcal{D}_2\)'-t Dandelin-gömböket.
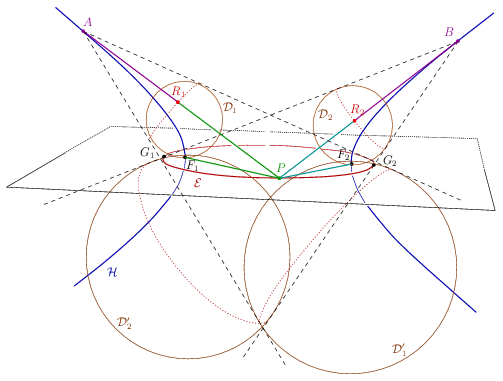
Legyen most az \(\displaystyle AP\) alkotó érintési pontja a \(\displaystyle \mathcal{D}_1\) gömbön \(\displaystyle R_1\), a \(\displaystyle BP\) alkotó érintési pontja a \(\displaystyle \mathcal{D}_2\) gömbön \(\displaystyle R_2\). A \(\displaystyle P\) pontból a gömbökhöz húzott érintők egyenlőségéből \(\displaystyle PR_1=PF_1\) és \(\displaystyle PR_2=PF_2\), így
\(\displaystyle PA+PB = (AR_1+PR_1)+(BR_2+PR_2) = AR_1 + BR_2 + (PF_1+PF_2). \)
A kúpok forgásszimmetriája miatt sem az \(\displaystyle AR_1\), sem az \(\displaystyle BR_2\) távolság nem függ \(\displaystyle P\) választásától, és az \(\displaystyle F_1,F_2\) fókuszú ellipszisen \(\displaystyle PF_1+PF_2\) állandó. Ezzel igazoltuk az állítást.
Statisztika:
25 dolgozat érkezett. 6 pontot kapott: Dobák Dániel, Döbröntei Dávid Bence, Gáspár Attila, Hervay Bence, Jánosik Áron, Janzer Orsolya Lili, Nagy Nándor, Pituk Gábor, Richlik Róbert, Schifferer András, Schrettner Jakab, Shuborno Das, Szabó 417 Dávid, Weisz Máté, Zsigri Bálint. 5 pontot kapott: Szabó 864 Blanka, Szabó 997 Balázs István, Szécsényi Nándor. 4 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2018. januári matematika feladatai

