A B. 4969. feladat (2018. szeptember)

B. 4969. A $\displaystyle T$ téglalap oldalai $\displaystyle a\le b$. Tudjuk, hogy valamely két $\displaystyle r$ sugarú kör együttesen lefedi $\displaystyle T$-t, valamint azt is tudjuk, hogy két $\displaystyle r$-nél kisebb sugarú körrel ez nem lehetséges. Határozzuk meg $\displaystyle r$-t.

(4 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

Megoldás. Legyenek $\displaystyle AB=CD=b$ és $\displaystyle BC=DA=a$, az $\displaystyle AB$, $\displaystyle CD$ és $\displaystyle DA$ oldalak felezőpontjai pedig rendre $\displaystyle E$, $\displaystyle F$ és $\displaystyle G$ (az ábra szerint).

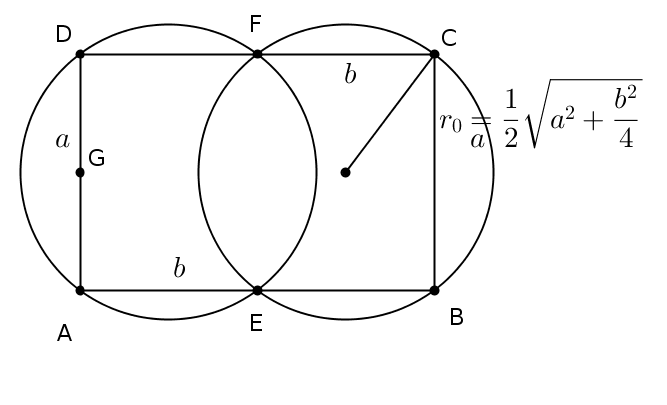
Az $\displaystyle AEFD$ és $\displaystyle FEBC$ téglalapok körülírt köreinek sugara (Pitagorasz tétele alapján) $\displaystyle r_0 = \dfrac{1}{2} \sqrt{a^2+\dfrac{b^2}{4}}$. Ezek a körök együttesen lefedik $\displaystyle ABCD$-t, ezért $\displaystyle 2r \leq \sqrt{a^2+\dfrac{b^2}{4}}=2r_0$.

Megmutatjuk, hogy szükségképpen $\displaystyle r\geq r_0$ is teljesül. Tegyük fel, hogy valamely $\displaystyle k_1$ és $\displaystyle k_2$ $\displaystyle r$ sugarú körök együttesen lefedik $\displaystyle T$-t. (Felhasználjuk, hogy $\displaystyle k_1$ és $\displaystyle k_2$ szerepe szimmetrikus.)

Ha $\displaystyle k_1$ kör tartalmazza $\displaystyle T$ három csúcsát, akkor két szemköztit is, így átmérője legalább $\displaystyle 2r \geq \sqrt{a^2+b^2}>2r_0$.

Tegyük fel a továbbiakban, hogy $\displaystyle k_1$ csak a $\displaystyle T$ két szomszédos csúcsát tartalmazza, vagy $\displaystyle A$-t és $\displaystyle B$-t, vagy $\displaystyle A$-t és $\displaystyle D$-t.

1. eset. Ha $\displaystyle k_1$ $\displaystyle A$-t és $\displaystyle B$-t (és így $\displaystyle k_2$ $\displaystyle C$-t és $\displaystyle D$-t) tartalmazza, akkor valamelyik kör, mondjuk $\displaystyle k_1$, tartalmazza $\displaystyle G$-t, ezért átmérője $\displaystyle 2r\geq BG= \sqrt{b^2+\dfrac{a^2}{4}}$, amire ($\displaystyle a\leq b$ miatt) $\displaystyle 2r\geq \sqrt{b^2+\dfrac{a^2}{4}}\geq \sqrt{a^2+\dfrac{b^2}{4}}=2r_0$.

2. eset. Ha $\displaystyle k_1$ csak az $\displaystyle A$ és $\displaystyle D$ (és így $\displaystyle k_2$ $\displaystyle B$ és $\displaystyle C$) csúcsokat tartalmazza, akkor valamelyik kör, mondjuk $\displaystyle k_1$, tartalmazza $\displaystyle E$-t, ezért átmérője $\displaystyle 2r\geq DE=\sqrt{a^2+\dfrac{b^2}{4}}=2r_0$.

Vagyis valóban azt kaptuk, hogy $\displaystyle \boxed{\: r = \dfrac{1}{2} \sqrt{a^2+\dfrac{b^2}{4}} \:}$  .

Statisztika:

180 dolgozat érkezett.
4 pontot kapott:	51 versenyző.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	21 versenyző.
1 pontot kapott:	75 versenyző.
0 pontot kapott:	18 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	4 dolgozat.

A KöMaL 2018. szeptemberi matematika feladatai