 |
A B. 4970. feladat (2018. szeptember) |
B. 4970. Adott a síkon két pont \(\displaystyle A\) és \(\displaystyle B\), továbbá egy ezeket elválasztó \(\displaystyle e\) egyenes. Válasszunk az \(\displaystyle e\) egyenesen \(\displaystyle P\) és \(\displaystyle Q\) pontokat úgy, hogy \(\displaystyle PAQ\sphericalangle=90^{\circ}\) teljesüljön. Mutassuk meg, hogy létezik egy olyan, \(\displaystyle B\)-től különböző pont, amelyen a \(\displaystyle B\), \(\displaystyle P\) és \(\displaystyle Q\) pontokra illeszkedő kör — a \(\displaystyle P\) és \(\displaystyle Q\) pontok választásától függetlenül — áthalad.
Javasolta: 11. C. osztály, Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn.
(5 pont)
A beküldési határidő 2018. október 10-én LEJÁRT.
Megoldás.
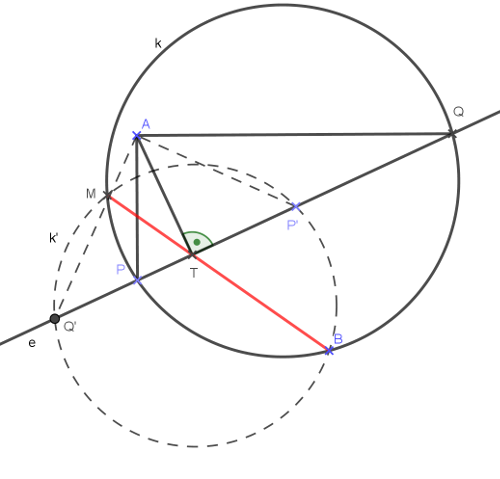
Legyen az \(\displaystyle APQ\) derékszögű háromszög átfogóhoz tartozó magasságának talppontja az \(\displaystyle e\) egyenesen a \(\displaystyle T\) pont. A magasságtétel alapján
\(\displaystyle PT \cdot TQ =AT^2.\)
Ez a szorzat a \(\displaystyle P\) és \(\displaystyle Q\) pontok összes lehetséges helyzetére ugyanez az \(\displaystyle AT^2\), vagyis állandó. Vegyünk most egy olyan \(\displaystyle k\) kört, amely átmegy a \(\displaystyle P, B\) és \(\displaystyle Q\) pontokon és hosszabbítsuk meg a \(\displaystyle TB\) szakaszt úgy, hogy messe még egy pontban, az \(\displaystyle M\) pontban a \(\displaystyle k\) kört. A \(\displaystyle k\) kör \(\displaystyle T\) pontra vonatkozó hatványa alapján
\(\displaystyle PT \cdot TQ=BT \cdot TM=AT^2=\text{áll}. \)
Az \(\displaystyle M\) pont helyzetét a rögzített \(\displaystyle A, T\) és \(\displaystyle B\) pontok egyértelműen meghatározák, ennek helyzete nem függ a \(\displaystyle P\) és \(\displaystyle Q\) megválasztásától. Az \(\displaystyle M\) pont mindegyik megfelelő \(\displaystyle k\) körön rajta van.
Statisztika:
56 dolgozat érkezett. 5 pontot kapott: Apagyi Dávid, Baski Bence, Beke Csongor, Bencsik Ádám, Bokor Endre, Bukva Dávid, Bursics András, Csertán András, Csiszár Zoltán, Deák Bence, Dobák Dániel, Espán Márton, Fajszi Bulcsú, Fekete Richárd, Fitos Bence, Fraknói Ádám, Fülöp Anna Tácia, Füredi Erik Benjámin, Győrffi Ádám György, Győrffy Ágoston, Győrffy Johanna, Hámori Janka, Hervay Bence, Hoffmann Balázs, Jedlovszky Pál, Keltai Dóra, Kerekes Anna, Kitschner Bernadett, Le Julianna Phuonglinh, Márton Dénes, Nagy Nándor, Nguyen Bich Diep, Noszály Áron, Rareș Polenciuc, Soós 314 Máté, Szabó 417 Dávid, Szabó 991 Kornél, Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Velich Nóra, Weisz Máté, Zsigri Bálint. 4 pontot kapott: Daniel Ghenghea. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2018. szeptemberi matematika feladatai
