 |
A B. 4977. feladat (2018. október) |
B. 4977. Bizonyítsuk be, hogy egy derékszögű háromszög beírt körének érintési pontjai által meghatározott háromszög magasságpontja a derékszögű háromszög átfogójához tartozó magasságvonalára illeszkedik.
(Kvant)
(4 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. Tegyük fel, hogy az \(\displaystyle ABC\) háromszögben a \(\displaystyle C\) csúcsnál lévő szög, \(\displaystyle γ= 90°\); \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) a beírt körnek a \(\displaystyle BC\), \(\displaystyle AC\), illetve \(\displaystyle AB\) oldalon lévő érintési pontjai; végül \(\displaystyle CH\) az átfogóhoz tartozó magasság. A külső pontból körhöz húzott érintőszakaszok egyenlősége miatt \(\displaystyle AB'=AC'\), így az \(\displaystyle AC'B'\triangle\) egyenlő szárú, és \(\displaystyle AC'B'\angle=AB'C'\angle\). Messe az \(\displaystyle A'B'C'\) háromszög \(\displaystyle A'\)-ből induló magasságvonala \(\displaystyle CH\)-t \(\displaystyle M\)-ben.
Mivel \(\displaystyle CH\perp AC'\) és \(\displaystyle A'M\perp B'C'\), így \(\displaystyle AC'B'\angle\) és \(\displaystyle CMA'\angle\) merőleges szárú szögek, ezért \(\displaystyle CMA'\angle=AC'B'\angle\). Hasonlóan \(\displaystyle MA'C\angle\) és \(\displaystyle C'B'A\angle\) is merőleges szárú szögpár, hiszen \(\displaystyle A'C\perp AB'\) és \(\displaystyle A'M\perp C'B'\), így \(\displaystyle MA'C\angle=C'B'A\angle\). Az eddigiekből következik, hogy \(\displaystyle MA'C\angle=C'B'A\angle=AC'B'\angle=CMA'\angle\), így \(\displaystyle CM=A'C\).
Legyen \(\displaystyle M'\) az \(\displaystyle A'B'C'\) háromszög \(\displaystyle B'\)-ből induló magasságvonalának és \(\displaystyle CH\)-nak a metszéspontja. A fenti gondolatmenethez analóg módon kapjuk, hogy \(\displaystyle CM'=B'C\). Ismét a külső pontból körhöz húzott érintők egyenlősége miatt \(\displaystyle CB'=CA'\), és így \(\displaystyle CM=CM'\) következik, ami miatt \(\displaystyle M=M'\). Ezzel megmutattuk, hogy a \(\displaystyle A'B'C'\) háromszög \(\displaystyle A'\)-ből, ill. \(\displaystyle B'\)-ből induló magasságai \(\displaystyle CH\)-n metszik egymást, így az állítást beláttuk.
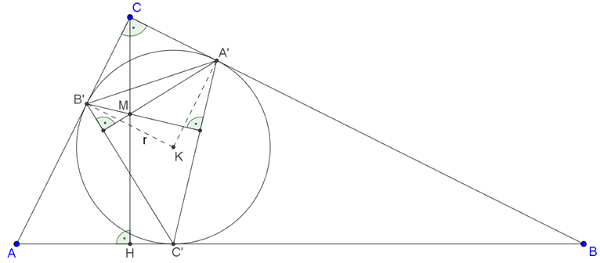
Megjegyzés. Ha \(\displaystyle K\) az \(\displaystyle ABC\) háromszög beírt körének középpontja, és \(\displaystyle r\) a sugara, akkor a \(\displaystyle KA'CB'\) négyszög egy négyzet. Ezért a fenti megoldásból következik, hogy \(\displaystyle CM= r\).
Statisztika:
69 dolgozat érkezett. 4 pontot kapott: Al-Hag Máté Amin, Apagyi Dávid, Bánó Bulcsú, Baski Bence, Beke Csongor, Bencsik Ádám, Biczó Benedek, Bokor Endre, Bukva Dávid, Bursics András, Csaplár Viktor, Csertán András, Csiszár Zoltán, Csizmadia Miklós, Dobák Dániel, Farkas Boróka, Fekete Richárd, Füredi Erik Benjámin, Geretovszky Anna, Gyetvai Miklós, Győrffi Ádám György, Győrffy Ágoston, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Keltai Dóra, Kerekes Anna, Kerekes Boldizsár, Kitschner Bernadett, Lovas Márton, Markó Gábor, Márton Dénes, Nagy 551 Levente, Nagy Nándor, Nguyen Bich Diep, Rareș Polenciuc, Sándor Péter, Sebestyén Pál Botond, Soós 314 Máté, Stomfai Gergely, Szabó 417 Dávid, Telek Zsigmond , Tiderenczl Dániel, Tóth 827 Balázs, Tóth Ábel, Tubak Dániel, Várkonyi Zsombor, Velich Nóra, Weisz Máté, Zsigri Bálint. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 6 versenyző.
A KöMaL 2018. októberi matematika feladatai

