 |
A B. 4991. feladat (2018. december) |
B. 4991. Artúr és Blanka egy kocka éleit felváltva pirosra festik úgy, hogy minden lépésben olyan élt színeznek ki, amely kitérő az utolsó lépésben kifestett élhez. A színezést Artúr kezdi. Az veszít, aki nem tud lépni. Kinek van nyerő stratégiája?
(3 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Megmutatjuk, hogy Blanka tud győzni. Ehhez a kocka tizenkét élét hat párba rendezzük úgy, hogy az egyes párokban szereplő élek egymáshoz kitérőek. Így Artúr minden lépése után Blanka ki tudja színezni a (még nyilvánvalóan színezetlen) párját, tehát nem fordulhat elő, hogy ne tudjon lépni. Ezért Artúr előbb-utóbb veszíteni fog, hiszen a játék legfeljebb 12 lépés után biztosan véget ér, tehát Blanka tényleg győz.
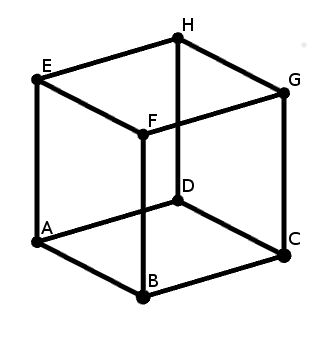
Megadunk egy a stratégiához szükséges lehetséges párosítást. Tekintsük a kocka csúcsainak az ábrán szereplő betűzését. Könnyű leellenőrizni, hogy az \(\displaystyle (AB,EH)\), \(\displaystyle (BC,EF)\), \(\displaystyle (CD, BF)\), \(\displaystyle (AD, GC)\), \(\displaystyle (AE, HG)\) és \(\displaystyle (DH, FG)\) párokban az élek egymáshoz kitérőek, és valóban a kocka mind a 12 éle pontosan egyszer szerepel.
Ezzel beláttuk, hogy Blankának van nyerő stratégiája.
Statisztika:
64 dolgozat érkezett. 3 pontot kapott: Argay Zsolt, Baski Bence, Bencsik Ádám, Bognár 171 András Károly, Csaplár Viktor, Csertán András, Dezső Kende Barnabás, Dobák Dániel, Fraknói Ádám, Fülöp Csilla, Füredi Erik Benjámin, Gyetvai Miklós, Hervay Bence, Jánosik Máté, Kerekes Boldizsár, Kocsis Anett, Kovács 129 Tamás, Kulcsár Boglárka, Laki Anna, Lovas Márton, Mátravölgyi Bence, Miszler Levente, Rareș Polenciuc, Soós 314 Máté, Telek Zsigmond , Tiszay Dávid, Tóth 057 Bálint, Tóth 827 Balázs, Tóth Ábel, Tóth-Rohonyi Iván, Várkonyi Zsombor, Zsigri Bálint. 2 pontot kapott: Apagyi Dávid, Bukva Dávid, Csizmadia Miklós, Fleiner Zsigmond, Kerekes Anna, Kitschner Bernadett, Kun Ágoston , Németh Norbert Marcell, Nyárfádi Patrik, Páhán Anita Dalma, Sárvári Tibor, Sebestyén Pál Botond, Seláf Bence, Szabó 991 Kornél, Tiszay Ádám, Velich Nóra. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 9 versenyző.
A KöMaL 2018. decemberi matematika feladatai

