Problem B. 5006. (February 2019)

B. 5006. The bases of a trapezium \(\displaystyle ABCD\) are \(\displaystyle AB\) and \(\displaystyle CD\), the intersection of the diagonals is \(\displaystyle M\). Diagonal \(\displaystyle AC\) bisects the angle \(\displaystyle BAD\), \(\displaystyle AM=BC\) and \(\displaystyle BM=CD\). Find the angles of the trapezium.

Based on a problem of the National Competition

(4 pont)

Deadline expired on March 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle DAC\measuredangle=CAB\measuredangle=ACD\measuredangle=\alpha\), \(\displaystyle ABD\measuredangle=BDC\measuredangle=\beta\) és \(\displaystyle DBC\measuredangle=\gamma\).

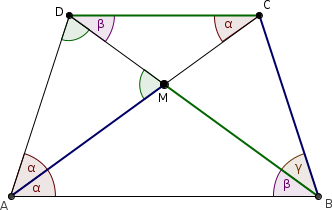
Az \(\displaystyle AMB\) és \(\displaystyle BCD\) háromszögekben \(\displaystyle AM=BC\), \(\displaystyle BM=CD\) és \(\displaystyle ABM\measuredangle=CDB\measuredangle\). Tehát két oldal, és az egyikkel szemközti szög megegyezik. Ez csak úgy lehetséges, ha (1) a másik oldallal szemközti szögek is megegyeznek, vagyis \(\displaystyle \alpha=\gamma\) (és a két háromszög egybevágó), vagy (2) a két szög összege \(\displaystyle \alpha+\gamma=180^\circ\). (Ugyanezt leolvashatjuk abból is, ha felírjuk a szinusztételt a két háromszögre: \(\displaystyle \frac{\sin\alpha}{\sin\beta}=\frac{BM}{AM}=\frac{CD}{BC}=\frac{\sin\gamma}{\sin\beta}\), tehát \(\displaystyle \sin\alpha=\sin\gamma\).)

Vegyük észre, hogy a \(\displaystyle BCD\) háromszögben \(\displaystyle DBC\measuredangle=\gamma\) és \(\displaystyle BCD\measuredangle>MCD\measuredangle=\alpha\), ezért \(\displaystyle \alpha+\gamma < BCD\measuredangle+DBC\measuredangle<180^\circ\), így a (2) eset nem lehetséges.

Az (1) esetben \(\displaystyle DAC\measuredangle=\alpha=\gamma=DBC\measuredangle\); ebből látjuk, hogy a trapéz húrtrapéz, így szimmetrikus is; a szimmetria miatt most már \(\displaystyle \alpha=\beta=\gamma\) és \(\displaystyle AM=BM=AD\). Az \(\displaystyle ABM\), és a szintén egyenlő szárú \(\displaystyle AMD\) háromszög szögeinek összeszámolásából \(\displaystyle ADM\measuredangle=AMD\measuredangle=2\alpha\), illetve \(\displaystyle 180^\circ=DAM\measuredangle+MDA\measuredangle+ADM\measuredangle=5\alpha\), tehát \(\displaystyle \alpha=36^\circ\). A trapéz szögei \(\displaystyle DAB\measuredangle=ABC\measuredangle=72^\circ\) és \(\displaystyle BCD\measuredangle=CDA\measuredangle=108^\circ\).

Diszkusszió: A megoldás teljességéhez annak igazolása is szükséges, hogy a feltételeknek eleget tevő trapéz létezik. Abban a szimmetrikus trapézban, amelyben \(\displaystyle BC=CD=AD\) és a szögei a fenti nagyságúak, az \(\displaystyle ACD\) és \(\displaystyle BCD\) egyenlő szárú háromszögekből láthatjuk, hogy \(\displaystyle DAC\measuredangle=ACD\measuredangle=DBC\measuredangle=CDB\measuredangle=36^\circ\); a trapéz \(\displaystyle A\) és \(\displaystyle B\) csúcsánál lévő szögeiből így \(\displaystyle MAB\measuredangle=ABM\measuredangle=36^\circ\); az \(\displaystyle ABM\) és \(\displaystyle ABD\) háromszögekből \(\displaystyle MDA\measuredangle=AMD\measuredangle=72^\circ\), emiatt az \(\displaystyle AMD\) háromszög egyenlő szárú, és \(\displaystyle BM=AM=AD=BC=CD\). Ez a trapéz tehát teljesíti a feltételekben leírt tulajdonságokat.

Statistics:

67 students sent a solution.
4 points:	Ajtai Boglárka, Apagyi Dávid, Bánó Bulcsú, Baski Bence, Beke Csongor, Bokor Endre, Csaplár Viktor, Farkas Boróka, Fleiner Zsigmond, Fraknói Ádám, Fülöp Anna Tácia, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Hámori Janka, Hegedűs Dániel, Hervay Bence, Jánosik Áron, Kerekes Anna, Kerekes Boldizsár, Kisida Júlia, Kitschner Bernadett, Kovács 129 Tamás, Lengyel Ádám, Lovas Márton, Markó Gábor, Mátravölgyi Bence, Nagy 551 Levente, Nagy Nándor, Nguyen Bich Diep, Osztényi József, Rareș Polenciuc, Richlik Róbert, Sebestyén Pál Botond, Soós 314 Máté, Szabó 991 Kornél, Tálos Zoltán, Telek Zsigmond , Tiderenczl Dániel, Tóth 057 Bálint, Tóth 827 Balázs, Török Ágoston, Várkonyi Zsombor, Velich Nóra, Weisz Máté, Zsigri Bálint.
3 points:	11 students.
2 points:	3 students.
1 point:	7 students.

Problems in Mathematics of KöMaL, February 2019