 |
A B. 5010. feladat (2019. február) |
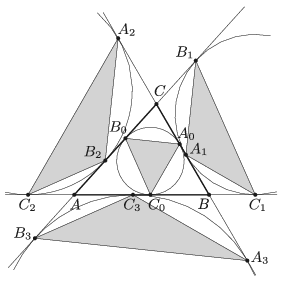
B. 5010. Egy hegyesszögű \(\displaystyle ABC\) háromszög beírt köre az oldalakat az \(\displaystyle A_0\), \(\displaystyle B_0\) és \(\displaystyle C_0\) pontokban érinti. A háromszög három hozzáírt körének érintési pontjai az oldalegyeneseken rendre \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\); \(\displaystyle A_2\), \(\displaystyle B_2\) és \(\displaystyle C_2\); illetve \(\displaystyle A_3\), \(\displaystyle B_3\) és \(\displaystyle C_3\). Az \(\displaystyle A_iB_iC_i\) háromszög területét jelölje \(\displaystyle T_i\) (\(\displaystyle i=0,1,2,3\)). Mutassuk meg, hogy
\(\displaystyle \frac{1}{T_0}=\frac{1}{T_1}+\frac{1}{T_2}+\frac{1}{T_3}. \)
(5 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. Jelölje az \(\displaystyle A_iB_iC_i\) kör sugarát \(\displaystyle r_i\), középpontját \(\displaystyle I_i\), az ábra szerint. Jelöljük a szokásos módon \(\displaystyle a\)-val, \(\displaystyle b\)-vel és \(\displaystyle c\)-vel, ill. \(\displaystyle \alpha\)-val, \(\displaystyle \beta\)-val és \(\displaystyle \gamma\)-val az \(\displaystyle ABC\) háromszög oldalait, ill. belső szögeit; továbbá legyen \(\displaystyle R\), \(\displaystyle s\) és \(\displaystyle T\) rendre az \(\displaystyle ABC\triangle\) körülírt körének sugara, félkerülete és területe.
Először is emlékeztetünk a jól ismert területképletekre: \(\displaystyle T=r_0s=r_1(s-a)=r_2(s-b)=r_3(s-c)\) (lásd pl. Kiss György KöMaL-cikkében a 8. állítást). Ezekből azonnal következik, hogy \(\displaystyle r_0/r_1=(s-a)/s\), \(\displaystyle r_0/r_2=(s-b)/s\) és \(\displaystyle r_0/r_3=(s-c)/s\). Végül ezeket összegezve
| \(\displaystyle \frac{r_0}{r_1}+\frac{r_0}{r_2}+\frac{r_0}{r_3}=\frac{(s-a)+(s-b)+(s-c)}{s}=\frac s s=1,\) | \(\displaystyle (1)\) |
azaz a beírt és hozzáírt körök sugaraira az állításra nagyon hasonlító összefüggés teljesül (az imént idézett cikk 9. állítása).
Megmutatjuk, hogy \(\displaystyle T_0/T_1=r_0/r_1\), \(\displaystyle T_0/T_2=r_0/r_2\) és \(\displaystyle T_0/T_3=r_0/r_3\). Ezekből az állítás az (1) összefüggés miatt következik. Nyilván elegendő a \(\displaystyle T_0/T_1=r_0/r_1\) egyenlőséget igazolni, a másik kettő analóg módon bizonyítható.
Először vegyük észre, hogy \(\displaystyle T_0=T_{I_0A_0B_0}+T_{I_0B_0C_0}+T_{I_0C_0A_0}\) és \(\displaystyle T_1=T_{I_1A_1B_1}-T_{I_1B_1C_1}+T_{I_1C_1A_1}\). A felbontásokban szereplő egyenlő szárú háromszögek területeit felírhatjuk szárszögük segítségével, pl. \(\displaystyle T_{I_0A_0B_0}=r_0^2\sin(180^\circ - \gamma)/2=r_0^2\sin \gamma/2\), \(\displaystyle T_{I_1A_1B_1}=r_1^2\sin \gamma /2\) és \(\displaystyle T_{I_1B_1C_1}=r_1^2\sin (\beta +\gamma) /2=r_1^2\sin \alpha /2\). (A megfelelő szárszögek kiszámítását az olvasóra bízzuk.) Ezek alapján
| \(\displaystyle \frac{T_0}{T_1}=\frac{r_0^2\sin \gamma/2+r_0^2\sin \beta /2+r_0^2\sin \alpha/2}{r_1^2\sin \gamma /2+r_1^2\sin \beta /2-r_1^2\sin \alpha /2}=\frac{r_0}{r_1}\cdot \frac{r_0(\sin \alpha+\sin \beta +\sin \gamma)}{r_1(\sin \beta+\sin \gamma -\sin \alpha)}.\) | \(\displaystyle (2)\) |
Felhasználva a fentebb igazolt \(\displaystyle r_0/r_1=(s-a)/s\) összefüggést és a sinus-tételt kapjuk, hogy
\(\displaystyle \frac{r_0(\sin \alpha+\sin \beta +\sin \gamma)}{r_1(\sin \beta+\sin \gamma -\sin \alpha)}=\frac{s-a}{s}\cdot \frac{\frac a{2R}+\frac b{2R}+\frac c{2R}}{\frac b{2R}+ \frac c{2R}-\frac a{2R}}=\frac{s-a}{s}\cdot \frac{2s}{2s-2a}=1, \)
amiből (2) miatt következik, hogy \(\displaystyle T_0/T_1=r_0/r_1\), ahogy állítottuk. Ezzel a bizonyítást befejeztük.
Megjegyzés. A \(\displaystyle T_0\) és \(\displaystyle T_1\) (ill. \(\displaystyle T_2\) és \(\displaystyle T_3\)) területek kiszámításánál felhasználtuk azt az ismert tényt, hogy a beírt kör \(\displaystyle I_0\) középpontja benne van az \(\displaystyle A_0B_0C_0\) háromszögben, míg a hozzáírt körök \(\displaystyle I_1\), \(\displaystyle I_2\) és \(\displaystyle I_3\) középpontjai nincsenek benne a megfelelő \(\displaystyle A_iB_iC_i\) háromszögekben. Másképpen mondva, felhasználtuk, hogy az \(\displaystyle A_0B_0C_0\) háromszög hegyesszögű, míg a többi \(\displaystyle A_iB_iC_i\) háromszög tompaszögű.
Ezt egyszerű szögszámolással igazolhatjuk: az \(\displaystyle AB_0C_0\) háromszög egyenlő szárú, ezért \(\displaystyle AC_0B_0\angle=90^\circ-\alpha/2\). Hasonlóan \(\displaystyle A_0C_0B\angle=90^\circ -\beta/2\), így \(\displaystyle B_0C_0A_0\angle=(\alpha+\beta)/2<(\alpha+\beta+\gamma)/2=90^\circ\). Hasonlóan belátható, hogy az \(\displaystyle A_0B_0C_0\triangle\) másik két csúcsánál is hegyesszög van.
Továbbá az \(\displaystyle AB_3C_3\triangle\) is egyenlő szárú, ezért \(\displaystyle AC_3B_3\angle=\alpha/2\). Hasonlóan \(\displaystyle BC_3A_3\angle=\beta/2\), így \(\displaystyle B_3C_3A_3\angle=180^\circ -\alpha/2-\beta/2>180^\circ- (\alpha+\beta+\gamma)/2=90^\circ \), azaz az \(\displaystyle A_3B_3C_3\triangle\) tompaszögű. Az \(\displaystyle A_1B_1C_1\triangle\) és \(\displaystyle A_2B_2C_2\triangle\) esetén hasonlóan érvelünk.
Statisztika:
32 dolgozat érkezett. 5 pontot kapott: Apagyi Dávid, Baski Bence, Beke Csongor, Bukva Dávid, Csaplár Viktor, Füredi Erik Benjámin, Geretovszky Anna, Győrffi Ádám György, Hámori Janka, Hegedűs Dániel, Jánosik Áron, Kerekes Anna, Kovács 129 Tamás, Nagy Nándor, Rareș Polenciuc, Stomfai Gergely, Telek Zsigmond , Tiderenczl Dániel, Tóth 827 Balázs, Weisz Máté, Zsigri Bálint. 4 pontot kapott: Asztalos Ádám, Kerekes Boldizsár, Kitschner Bernadett. 3 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2019. februári matematika feladatai

