A B. 5081. feladat (2020. február)

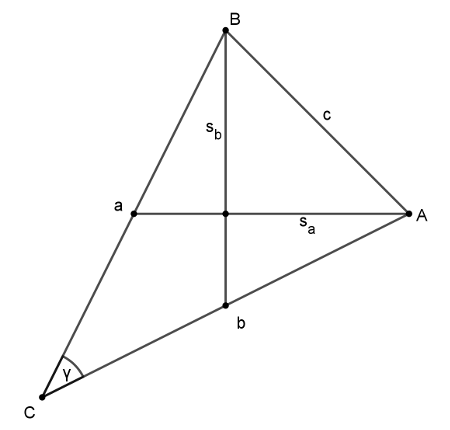
B. 5081. Egy háromszögben az \(\displaystyle a\) és \(\displaystyle b\) oldalakhoz tartozó súlyvonalak merőlegesek egymásra. Bizonyítsuk be, hogy \(\displaystyle \frac 12<\frac ab<2\).

(3 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Pitagorasz tétele és a paralelogramma-tétel szerint

\(\displaystyle c^2=\frac{4}{9}(s_a^2 + s_b^2)=\frac{(-a^2+2b^2+2c^2)+(2a^2-b^2+2c^2)}{9}=\frac{a^2+b^2+4c^2}{9}, \)

rendezve \(\displaystyle 5c^2=a^2+b^2\). A koszinusz-tétel alapján ez \(\displaystyle 5(a^2+b^2-2ab\cos\gamma)=a^2+b^2\). Mivel a súlyvonalak a háromszög belsejében haladnak, a megfelelő oldalak szögénél nagyobb szöget zárnak be; esetünkben ezért \(\displaystyle \cos\gamma < 1\). Így \(\displaystyle 1 > \cos\gamma = \frac{2}{5}\frac{a^2+b^2}{ab}= \frac{2}{5}(\frac{a}{b} + \frac{b}{a})\). Ez \(\displaystyle h:=\frac{a}{b}\)-re a másodfokú \(\displaystyle 0 > 2h^2-5h+2\) egyenlőtlenséget adja, melynek megoldása \(\displaystyle \frac{1}{2} < h < 2\).

Statisztika:

85 dolgozat érkezett.
3 pontot kapott:	71 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2020. februári matematika feladatai