A B. 5135. feladat (2020. december)

B. 5135. Az $\displaystyle ABC$ hegyesszögű háromszög $\displaystyle A$, $\displaystyle B$, $\displaystyle C$ csúcsaiból húzott magasságok talppontjai rendre $\displaystyle A_1$, $\displaystyle B_1$ és $\displaystyle C_1$; az $\displaystyle AA_1$ és $\displaystyle BB_1$ magasságok felezőpontjai pedig rendre $\displaystyle G$ és $\displaystyle H$. Igazoljuk, hogy a $\displaystyle C_1GH$ háromszög körülírt köre áthalad az $\displaystyle AB$ oldal $\displaystyle F$ felezőpontján.

Javasolta: Bíró Bálint (Eger)

(4 pont)

A beküldési határidő 2021. január 11-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit, legyen $\displaystyle M$ az $\displaystyle ABC$ háromszög magasságpontja. Megmutatjuk, hogy az $\displaystyle MF$ szakasz a $\displaystyle C_1$, $\displaystyle G$ és $\displaystyle H$ pontok mindegyikéből derékszög alatt látszik, ebből az állítás a Thalész-tétel megfordítása segítségével azonnal következik.

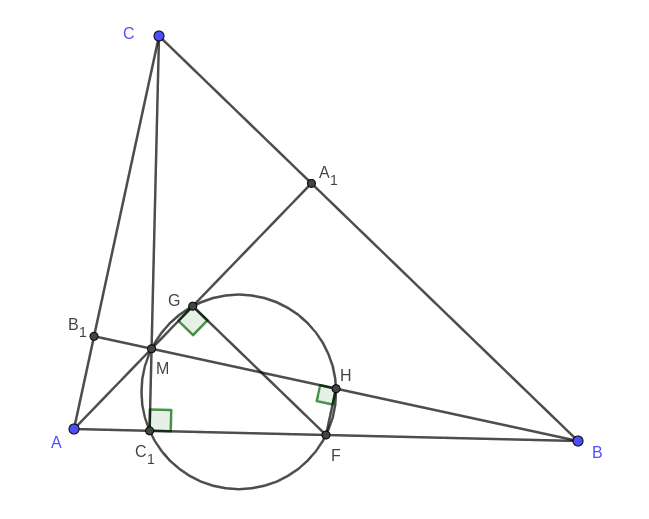
Mivel $\displaystyle M$ illeszkedik a $\displaystyle CC_1$ szakaszra, és $\displaystyle CC_1\perp AB$, így $\displaystyle MC_1F\angle$ valóban derékszög.

Az $\displaystyle ABA_1$ háromszögben $\displaystyle FG$ a $\displaystyle BA_1$ befogóval párhuzamos középvonal, így $\displaystyle FG\perp AA_1$, tehát $\displaystyle FGM\angle$ derékszög. Hasonlóan, az $\displaystyle ABB_1$ háromszögben $\displaystyle FH$ az $\displaystyle AB_1$ befogóval párhuzamos középvonal, ami miatt $\displaystyle FH\perp BB_1$, s így $\displaystyle FHM\angle$ is derékszög. Ezzel az állítást beláttuk.

Diszkusszió: a $\displaystyle C_1GH$ kör jól definiált, nyilvánvalóan $\displaystyle C_1\neq G$ és $\displaystyle C_1\neq H$; míg $\displaystyle G=H$ esetén az $\displaystyle ABA_1B_1$ négyszög átlói felezve metszenék egymást, azaz a négyszög paralelogramma lenne, s az $\displaystyle ABC$ háromszögnek lenne két párhuzamos oldala. A $\displaystyle C_1,G,H$ pontok tehát páronként különböznek. Továbbá $\displaystyle FG\parallel BA_1=BC$ és $\displaystyle FH\parallel AB_1=AC$ miatt a három pont nem eshet egy egyenesre.

A $\displaystyle C_1=F$, $\displaystyle G=M$ és $\displaystyle H=M$ esetekben a bizonyításban használt szögek esetleg nem jönnek létre, de a $\displaystyle C_1$, $\displaystyle G$ és $\displaystyle H$ pontok ilyenkor is nyilvánvalóan illeszkednek az $\displaystyle MF$ szakasz Thalész-körére.

Statisztika:

93 dolgozat érkezett.
4 pontot kapott:	Győrffi Ádám György, Horváth 530 Mihály, Kercsó-Molnár Anita, Nagy 551 Levente, Romaniuc Albert-Iulian, Szanyi Attila, Török Ágoston, Zömbik Barnabás.
3 pontot kapott:	64 versenyző.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2020. decemberi matematika feladatai