 |
A B. 5192. feladat (2021. október) |
B. 5192. Nyolc gyerek elhatározta, hogy az őszi szünet első hét napján egy-egy focimeccset játszanak, négy a négy ellen. Meg tudják-e úgy szervezni a meccseket, hogy bármelyik három gyerek legalább egyszer ugyanabban a csapatban játsszon?
Gáspár Merse Előd (Budapest) ötletéből
(5 pont)
A beküldési határidő 2021. november 10-én LEJÁRT.
Megoldás. Meg lehet így szervezni a meccseket. Ehhez adjunk a 8 gyerek mindegyikének egy háromjegyű, 0 és 1 számjegyekből álló azonosítószámot: \(\displaystyle 000, 001, 010, 011, 100, 101, 110, 111\).
Az első napon az egyik csapatba azok kerüljenek, akiknek 0-val kezdődik az azonosítószámuk, míg a másikba az 1-essel kezdődő számúak. A második napon aztán az azonosítószám második jegye alapján osztjuk őket két csapatra, végül a harmadik napon az utolsó jegy szerint. Tehát az első három meccs:
1. \(\displaystyle (000, 001, 010, 011)\) vs \(\displaystyle (100, 101, 110, 111)\).
2. \(\displaystyle (000, 001, 100, 101)\) vs \(\displaystyle (010, 011, 110, 111)\).
3. \(\displaystyle (000, 010, 100, 110)\) vs \(\displaystyle (001, 011, 101, 111)\).
A negyedik napon azok kerüljenek az egyik csapatba, akiknek a számának az első két számjegye egyforma, a másik csapatba pedig azok, akiknél ez a két számjegy különböző. Hasonlóképpen, az ötödik napon az első és a harmadik jegyet, míg a hatodik napon az utolsó két jegyet összehasonlítva alakulnak ki a csapatok. Tehát a 4., 5. és 6. meccs:
4. \(\displaystyle (000, 001, 110, 111)\) vs \(\displaystyle (010, 011, 100, 101)\).
5. \(\displaystyle (000, 010, 100, 111)\) vs \(\displaystyle (001, 011, 100, 110)\).
6. \(\displaystyle (000, 011, 100, 111)\) vs \(\displaystyle (001, 010, 101, 110)\).
Végül az utolsó meccsen azok játszanak az első csapatban, akiknek az azonosítószámában páros sok 1-es szerepel – értelemszerűen azok, akiknek páratlan sok 1-es van az azonosítószámában, a második csapatba kerülnek.
7. \(\displaystyle (000, 011, 101, 110)\) vs \(\displaystyle (001, 010, 100, 111)\).
Most bebizonyítjuk, hogy valóban teljesül bármely három gyerekre, hogy valamikor szerepeltek egy csapatban.
Indirekt tegyük fel, hogy van három gyerek, akikre ez nem teljesül. Ekkor az első számjegyeik között van két egyforma és egy ettől különböző (különben már az első napon együtt lettek volna). Nevezzük \(\displaystyle A\)-nak és \(\displaystyle B\)-nek azt a két gyereket, akiknek egyforma az első jegye, és \(\displaystyle C\)-nek a harmadikat. Mivel a második napon sem voltak együtt, ezért a második számjegyre is elmondható, hogy két gyereknek egyforma, és a harmadiknak különböző. Ha megint \(\displaystyle A\)-nak és \(\displaystyle B\)-nek lenne egyforma, és \(\displaystyle C\)-nek különböző, az azt jelentené, hogy a 4. meccsen együtt volt \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) is. Tehát \(\displaystyle A\) és \(\displaystyle B\) második jegye különbözik, az egyikük – az általánosság korlátozása nélkül felthető, hogy \(\displaystyle A\) – második jegye persze megegyezik \(\displaystyle C\) második számjegyével. A harmadik jegyet illetően is kell egy egyező pár, de ez csak \(\displaystyle B\) és \(\displaystyle C\) lehet (hiszen ha \(\displaystyle A\) és \(\displaystyle B\) harmadik jegye egyezne, akkor az 5. napon; ha \(\displaystyle A\) és \(\displaystyle C\) egyezne, akkor pedig a 6. napon került volna mindhárom gyerek egy csapatba.)
Tehát \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) közül bármely két gyerek azonosítószáma pontosan egy jegyben egyezik, azaz két jegyben különbözik. Tehát vagy ugyanannyi 1-es van bennük, vagy az egyikben kettővel több, mint a másikban. Mindkét esetben megegyezik az 1-esek számának paritása. Tehát a 7. napon mindhárom gyerek ugyanazon csapatban szerepelt.
Megjegyzések a megoldáshoz. 1. Érdemes megfigyelni, hogy a konstrukciónkban szereplő 14 négyfős csapat mindegyikére teljesül, hogy ha az első számjegy nem egyforma mindegyiküknél, akkor a csapat két játékosánál 0 és a másik kettőnél 1. Ugyanez igaz a második és a harmadik számjegyre is. Ez azt is jelenti, hogy bármely három emberhez könnyen meghatározható, hogy ki lesz az egyetlen negyedik, akivel egy csapatban szerepelhetnek. Például a 001, 101 és 111 alkotta trió mellé csak a 011 kerülhet.
Ez ad egy új módszert is annak ellenőrzésére, hogy tényleg minden trió szerepel közös csapatban valamelyik meccsen. Mivel a hozzájuk tartozó negyedik tag egyértelműen megmondható (és egyetlen négyfős csapat sem áll össze ismétlődően a bajnokság során), ezért az világos, hogy minden trió legfeljebb egyszer játszhat együtt. Egy négyfős csapatból 4 trió választható ki, így a 14 négyfős csapatban összesen \(\displaystyle 14 \cdot 4 = 56\) trió szerepel együtt, ami éppen \(\displaystyle \binom{8}{3}\), azaz az összes lehetséges trió száma. Tehát mindegyik trió össze kellett álljon egyszer.
2. Az azonosítószámok alapján a gyerekek megfelelthethetők egy egységkocka csúcsainak is, például 101 az \(\displaystyle (1,0,1)\) koordinátájú csúcsnak. Ekkor az első három napon a kocka átellenes lappárjai csapnak össze. A 4., 5. és 6. napon mindig két szemközti él 4 végpontja kerül egy csapatba. A 7. nap csapatait pedig úgy kapjuk meg, ha sakktáblaszerűen feketére és fehérre színezzük a kocka csúcsait.
3. Az azonosítószámokra tekinthetünk úgy is, mint a kételemű test felett értelmezett háromdimenziós vektorokra. Ennek a vektortérnek éppen ez a 8 eleme van. A konstrukcióban megadott csapatok éppen egy-egy síknak felelnek meg ebben a vektortérben, az egymás ellen játszó csapatok közös pont nélküli, azaz ,,párhuzamos'' síkok.
4. Válasszunk ki egy gyereket (pl. a 000 azonosítószámmal rendelkezőt), és vizsgáljuk meg a vele egy csapatban szereplő triókat. Ezek a triók egy 7-elemű alaphalmaz 7 darab 3-elemű részhalmazát jelentik. Teljesül rájuk, hogy az alaphalmaz bármely két eleme pontosan egyszer szerepel közös 3-elemű halmazban. A már a B.5181. feladat megoldásában is előkerül konfiguráció, az úgynevezett Fano-sík ezt éppen teljesíti.
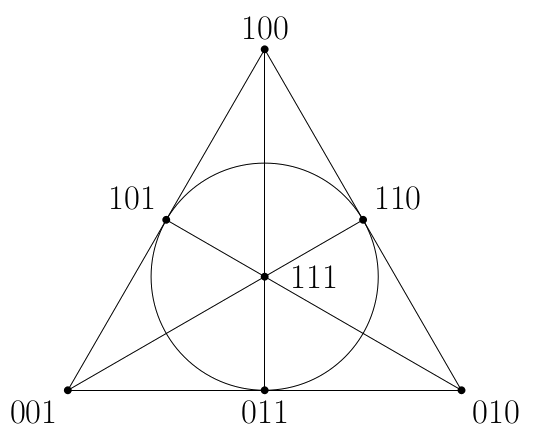
Sőt, azt sem nehéz belátni, hogy valójában a Fano-sík az egyetlen ilyen tulajdonságú konfiguráció. Ebből az is kiderül, hogy a feladat megoldása lényegében egyértelmű, azaz ha valaki megad 7 mérkőzést a feltételeknek megfelelően, akkor ki tudjuk osztani úgy az azonosítószámokat a diákok között, hogy a meccsek (valamilyen sorrendben) megegyezzenek a fenti konstrukcióban szereplő meccsekkel.
Statisztika:
171 dolgozat érkezett. 5 pontot kapott: 76 versenyző. 4 pontot kapott: 58 versenyző. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 2 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2021. októberi matematika feladatai

