A B. 5193. feladat (2021. október)

B. 5193. Az $\displaystyle ABC$ hegyesszögű háromszögben $\displaystyle BCA\sphericalangle=45^{\circ}$, a magasságok talppontjai a $\displaystyle BC$, $\displaystyle CA$, $\displaystyle AB$ oldalakon rendre $\displaystyle D$, $\displaystyle E$, $\displaystyle F$, a háromszög magasságpontja $\displaystyle M$. Tudjuk, hogy az $\displaystyle F$ pont az $\displaystyle AB$ szakaszt $\displaystyle {AF}:{FB}={2}:{3}$ arányban osztja. Az $\displaystyle AC$ oldalon megjelöljük azt a $\displaystyle G$ pontot, amelyre $\displaystyle CG=BM$. Mutassuk meg, hogy az $\displaystyle ABG$ háromszög súlypontja $\displaystyle M$.

(4 pont)

A beküldési határidő 2021. november 10-én LEJÁRT.

Megoldás.

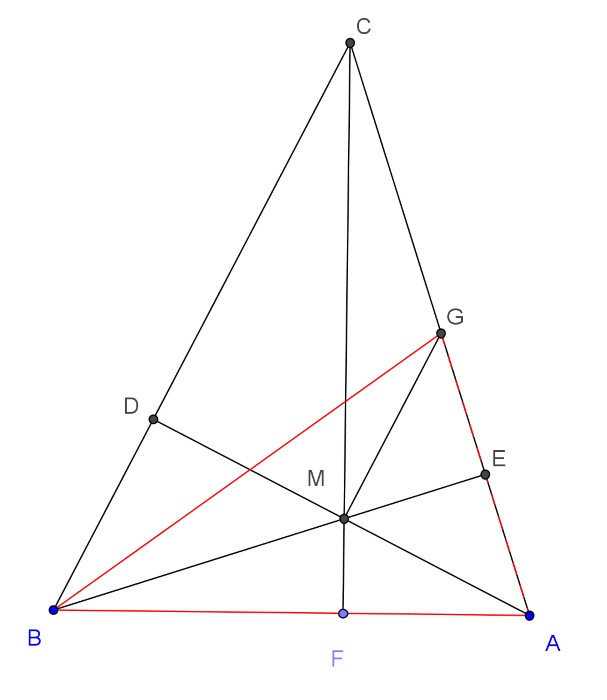
Az $\displaystyle ABC$ háromszög $\displaystyle C$-nél fekvő szöge $\displaystyle 45^{\circ}$, a $\displaystyle D$ és $\displaystyle E$ pontok magasságok talppontjai, így $\displaystyle CBE\sphericalangle=DAC\sphericalangle=45^{\circ}$. A $\displaystyle BMGC$ négyszög $\displaystyle BC$ oldalon fekvő szögei $\displaystyle 45^{\circ}$-osak, továbbá $\displaystyle BM=CG$, tehát a négyszög szimmetrikus trapéz. A trapéz $\displaystyle G$-nél fekvő külső szöge, az $\displaystyle AGM\sphericalangle=45^{\circ}$. Ezzel beláttuk, hogy $\displaystyle AGM$ egyenlő szárú háromszög, azaz $\displaystyle BE$ súlyvonala az $\displaystyle ABG$ egyenlő szárú háromszögnek. A bizonyítás befejezéséhez elegendő megmutatni, hogy az $\displaystyle M$ pont harmadolja az $\displaystyle EB$ szakaszt.

A szögek alapján $\displaystyle EM=AE$. Az $\displaystyle EMC$ és $\displaystyle EAB$ derékszögű háromszögekben egy-egy befogó és a velük szemközti szög is egyforma, a két háromszög egybevágó, vagyis $\displaystyle MC=AB$. Szintén a szögek alapján az is igaz, hogy $\displaystyle AEB\bigtriangleup \sim AFC\bigtriangleup$. Írjuk fel az eddigi megállapítások felhasználásával az $\displaystyle EM$ és $\displaystyle EB$ szakaszok $\displaystyle x$ arányát:

$\displaystyle x=\frac{EM}{EB}=\frac{AE}{EB}=\frac{AF}{FC}=\frac{AF}{AB+MF}.$

Az $\displaystyle AEB$ és $\displaystyle MFB$ derészögű háromszögek hasonlósága alapján pedig:

$\displaystyle x=\frac{EM}{EB}=\frac{EA}{EB}=\frac{MF}{FB}$

is teljesül. Ezzel kiegészítve a fentebbi gondolatmenetet:

$\displaystyle x=\frac{AF}{AB+MF}=\frac{AF}{AB+xBF}=\frac{\frac{2}{2}AB}{AB+x\cdot \frac{3}{5}AB}.$

Most az $\displaystyle AB$-vel egyszerűsítve rendezés után $\displaystyle x$-re másodfokú egyenletet kapunk:

$\displaystyle x=\frac{2}{5+3x},$

$\displaystyle 3x^2+5x-2=0.$

Az egyenlet pozitív gyöke $\displaystyle x=\frac{1}{3}$.

Beláttuk, hogy az $\displaystyle M$ pont az $\displaystyle ABG$ egyenlő szárú háromszög alaphoz tartozó magasságának harmadolópontja, tehát valóban a súlypont.

Statisztika:

97 dolgozat érkezett.
4 pontot kapott:	57 versenyző.
3 pontot kapott:	16 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2021. októberi matematika feladatai