A B. 5194. feladat (2021. október)

B. 5194. Az $\displaystyle ABC$ háromszögben $\displaystyle ABC\sphericalangle=2CAB\sphericalangle$. Az $\displaystyle AB$ oldal a beírt kört az $\displaystyle E$ pontban érinti, a $\displaystyle C$-ből induló szögfelezőt az $\displaystyle F$ pontban metszi. Igazoljuk, hogy $\displaystyle AF=2BE$.

(4 pont)

A beküldési határidő 2021. november 10-én LEJÁRT.

Megoldás. Legyenek az $\displaystyle ABC$ háromszög szögei a szokásos módon $\displaystyle \alpha$, $\displaystyle \beta$ és $\displaystyle \gamma$; a feltétel szerint $\displaystyle \beta=2\alpha$. Legyen az $\displaystyle AB$ oldalhoz hozzáírt kör középontja $\displaystyle J$, és a hozzáírt kör érintési pontja az $\displaystyle AB$ oldalon $\displaystyle E_1$. Jól ismert, hogy $\displaystyle AE_1=BE=s-b$, ahol $\displaystyle b=AC$ és $\displaystyle s$ az $\displaystyle ABC$ háromszög félkerülete.

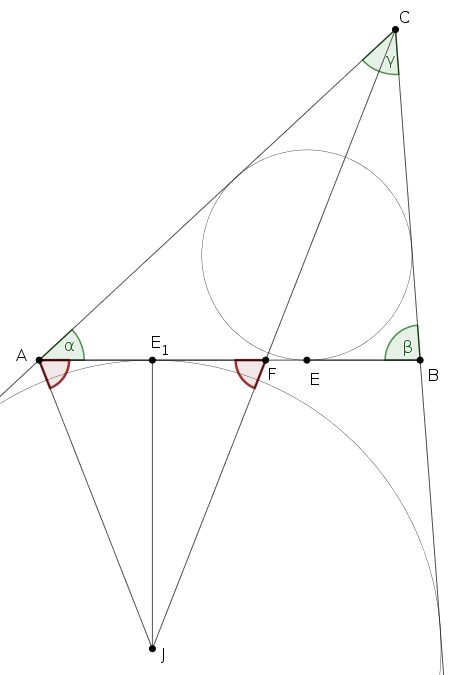
Az $\displaystyle A$-nál levő szögek összeszámolásából

$\displaystyle JAF\angle = \dfrac{180^\circ-BAC\angle}{2} = 90^\circ-\dfrac\alpha2,$

az $\displaystyle AFC$ háromszög szögeiből

$\displaystyle AFJ\angle = FAC\angle+ACF\angle = \alpha+\dfrac\gamma2 = \dfrac\beta2+\bigg(90^\circ-\dfrac\alpha2-\dfrac\beta2\bigg) = 90^\circ-\dfrac\alpha2 = JAF\angle.$

Tehát $\displaystyle AFJ\angle=JFA$; a $\displaystyle JFA$ háromszög egyenlő szárú, ezért

$\displaystyle AF = 2AE_1 = 2BE.$

Statisztika:

80 dolgozat érkezett.
4 pontot kapott:	65 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. októberi matematika feladatai