 |
A B. 5217. feladat (2022. január) |
B. 5217. Egy háromszög súlyvonalainak \(\displaystyle \frac{2}{\sqrt3}\)-szorosából mint oldalakból újabb háromszöget szerkesztünk. Az eljárást megismételjük a kapott háromszögre. Mutassuk meg, hogy a második lépésben az eredetivel egybevágó háromszöget kapunk.
Javasolta: Bártfai Pál (Budapest)
(4 pont)
A beküldési határidő 2022. február 10-én LEJÁRT.
Megoldás. Legyen \(\displaystyle ABC\) az adott háromszög, továbbá \(\displaystyle AB, BC, CA\) oldalainak felezőpontjai rendre a \(\displaystyle D, E\) és \(\displaystyle F\) pontok. Tükrözzük a háromszöget a \(\displaystyle BC\) oldal \(\displaystyle E\) felezőpontjára. Az \(\displaystyle A\) csúcs tükörképe \(\displaystyle A'\), az \(\displaystyle F\) felezőpont tükörképe az \(\displaystyle F'\) pont az ábra szerint.
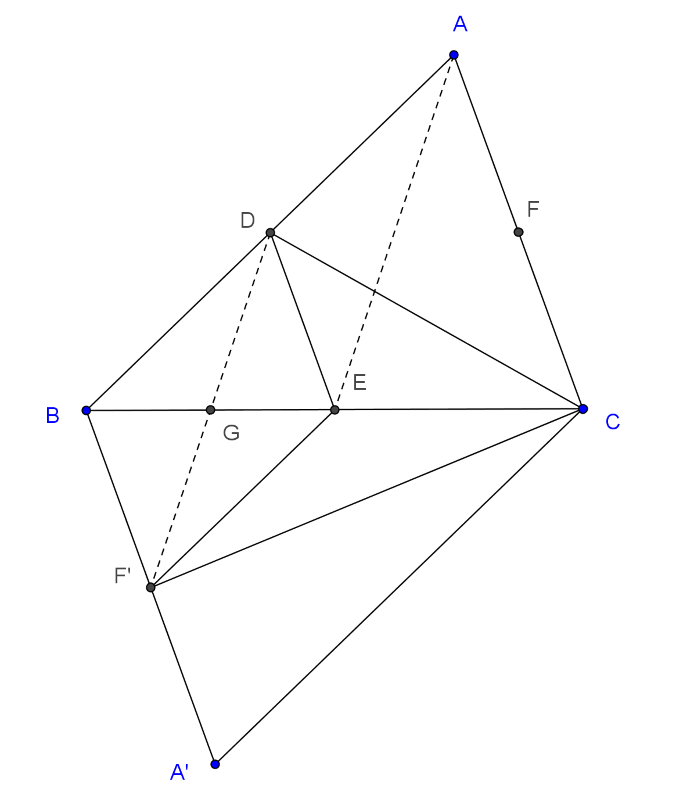
Megmutatjuk, hogy a \(\displaystyle DCF'\) háromszög oldalai az \(\displaystyle ABC\) háromszög súlyvonalaival egyező hosszúságúak. A \(\displaystyle DC\) szakasz az eredeti háromszögben az \(\displaystyle AB\) oldalhoz tartozó súlyvonal. A \(\displaystyle CF'\) szakasz az eredeti háromszög \(\displaystyle AF\) súlyvonalának tükörképe. Tekintsük most a \(\displaystyle DF'\) szakaszt. A \(\displaystyle BDEF'\) négyszög paralelogramma, mert a \(\displaystyle DE\) szakasz az \(\displaystyle ABC\) háromszög \(\displaystyle CA\) oldalhoz tartozó középvonala, míg a \(\displaystyle BF'\) szakasz a középpontosan tükrözött \(\displaystyle CA\) szakasz fele. Ennek megfelelően a \(\displaystyle BDEF'\) négyszög két szemközti oldala párhuzamos és egyenlő, így valóban paralelogrammáról van szó. Legyen átlóinak metszéspontja a \(\displaystyle G\) pont. Most tekintsük a \(\displaystyle DAEF'\) négyszöget. Az előzőekben beláttuk, hogy \(\displaystyle BD\#EF'\), így lévén \(\displaystyle D\) az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle DA\#EF'\), vagyis a \(\displaystyle DAEF'\) négyszög is paralelogramma, a \(\displaystyle DF'\) szakasz a háromszög harmadik súlyvonalával párhuzamos és egyenlő.
A bizonyítás befejezéséhez most vizsgáljuk a \(\displaystyle DCF'\), súlyvonalakból szerkesztett háromszög \(\displaystyle DF'\) oldalához tartozó súlyvonalát, a \(\displaystyle CG\) szakaszt. Mivel a \(\displaystyle G\) pont felezi a \(\displaystyle BE\) szakaszt, ezért a \(\displaystyle CG\) szakasz a \(\displaystyle BC\) oldal háromnegyede.
A \(\displaystyle BC\) oldalnak nem volt kitüntetett szerepe, így azonnal adódik az is, hogy a többi oldal felezőpontjára tükrözve, teljesen egyező módon belátható, hogy a súlyvonalból szerkesztett háromszög másik és harmadik oldalához tartozó súlyvonal is a megfelelő háromszög-oldal háromnegyede. A feladatban szereplő \(\displaystyle \lambda=\frac{2}{\sqrt{3}}\) arányú nagyítások miatt a kétszeri nagyítás után az eredeti oldalak \(\displaystyle \lambda^2\)-szeresét, \(\displaystyle \frac{4}{3}\)-szorosát kapjuk, vagyis az eredeti oldalhosszakat.
Megjegyzés: A súlyvonalakból szerkesztett háromszög súlyvonalainak hosszát két lépésben ki is tudjuk számolni.
Ismert, hogy a paralelogramma-tétel alapján az \(\displaystyle a, b, c\) oldalú háromszög \(\displaystyle a\)-hoz tartozó \(\displaystyle s_a\) súlyvonalára:
\(\displaystyle s_a^2=\frac{2b^2+2c^2-a^2}{4}.\)
Ugyanígy a másik két súlyvonalra:
\(\displaystyle s_b^2=\frac{2c^2+2a^2-b^2}{4}, \qquad s_c^2=\frac{2a^2+2b^2-c^2}{4}.\)
A súlyvonalak alkotta \(\displaystyle s_a, s_b, s_c\) háromszög \(\displaystyle s'_a\) súlyvonala:
\(\displaystyle s_a^{'2}=\frac{2s_b^2+2s_c^22-s_a^2}{4}= =\frac{2\frac{2c^2+2a_2-b^2}{4}+2\frac{2a^2+2b_2-c^2}{4}-\frac{2b^2+2c_2-a^2}{4}}{4}=\)
\(\displaystyle =\frac{4c^2+4a^2-2b^2+4a^2+4b^2-2c^2-2b^2-2c^2+a^2}{16}=\frac{9}{16}a^2.\)
Tehát \(\displaystyle s'_a=\frac{3}{4}a\). A kétszeri nagyítás után ismét kapjuk, hogy \(\displaystyle \lambda^2 s'_a=a\), továbbá a betűk cseréjével a másik szakaszra: \(\displaystyle \lambda^2 s'_b=b\), \(\displaystyle \lambda^2 s'_c=c\).
Statisztika:
90 dolgozat érkezett. 4 pontot kapott: Bálint Béla, Baski Bence, Ben Gillott, Bencsik Dávid, Bényei Borisz, Bognár 171 András Károly, Bognár Balázs, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Domján Olivér, Duchon Márton, Erdélyi Kata, Farkas 005 Bendegúz, Farkas 512 Izabella, Foris Dávid, Fülöp Csilla, Jánosik Máté, Kalocsai Zoltán, Kercsó-Molnár Anita, Koltai Csaba Ferenc, Kovács Dóra, László Anna, Melján Dávid Gergő, Mizik Lóránt, Mohay Lili Veronika, Móricz Benjámin, Nagy 429 Leila, Nguyen Kim Dorka, Páhán Anita Dalma, Rareș Polenciuc, Romaniuc Albert-Iulian, Seprődi Barnabás Bendegúz, Sipeki Márton, Somogyi Dalma, Szabó 248 Eszter, Szabó 810 Levente, Szakács Ábel, Szakács Domonkos, Szalontai Júlia, Tichy Márk, Tóth 057 Bálint, Tran Dávid, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás. 3 pontot kapott: 35 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. januári matematika feladatai
