A B. 5224. feladat (2022. február)

B. 5224. Az \(\displaystyle ABCD\) egységnégyzet \(\displaystyle BC\) oldalán úgy vesszük fel a \(\displaystyle P\) pontot, továbbá a \(\displaystyle CD\) oldalán a \(\displaystyle Q\) pontot, hogy \(\displaystyle PAQ\sphericalangle=45^{\circ}\). A \(\displaystyle P\) és \(\displaystyle Q\) pontok melyik helyzetében lesz \(\displaystyle BP+PQ+QD\) minimális?

Javasolta: Szoldatics József (Budapest)

(4 pont)

A beküldési határidő 2022. március 10-én LEJÁRT.

Megoldás. Legyen \(\displaystyle BAP\sphericalangle=\alpha\) és \(\displaystyle QAD\sphericalangle=\beta\) az ábra szerint. Tükrözzük az \(\displaystyle AB\) szakaszt az \(\displaystyle AP\) egyenesére és az \(\displaystyle AD\) szakaszt az \(\displaystyle AQ\) egyenesére. A \(\displaystyle B\) pont tükörképe \(\displaystyle B'\), a \(\displaystyle D\) pont tükörképe \(\displaystyle D'\).

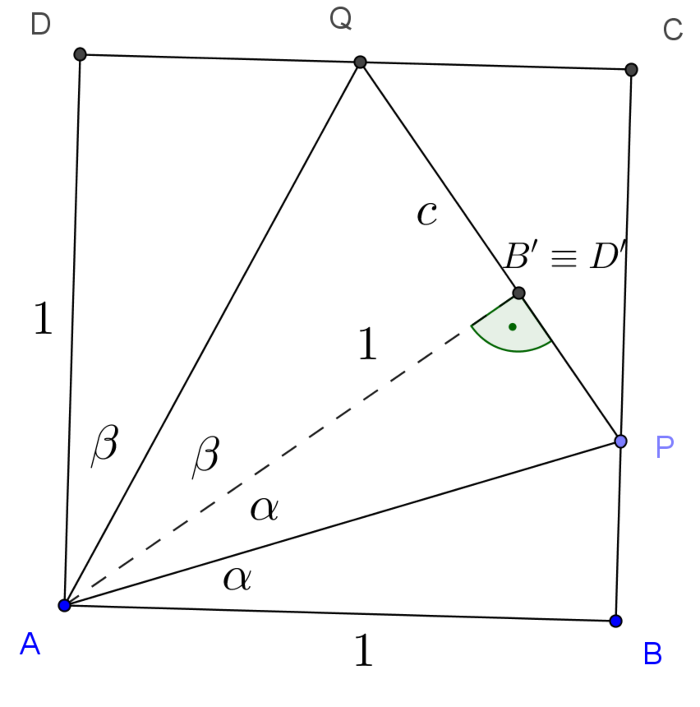
Mivel \(\displaystyle \alpha+\beta=45^\circ\), \(\displaystyle ABP\sphericalangle=ADQ\sphericalangle=90^\circ\) és \(\displaystyle AB=AD=1\) a \(\displaystyle B'\) és \(\displaystyle D'\) tükörképpontok egybeesnek, továbbá a \(\displaystyle PB'Q\sphericalangle\) egyenesszög, a \(\displaystyle P, B', Q\) pontok ebben a sorrendben egy egyenesen vannak. Ezzel látjuk, hogy a feladatban szereplő töröttvonal hossza kétszerese a \(\displaystyle PQ\) szakasz hosszának, vagy ha úgy tetszik a \(\displaystyle BP\) és \(\displaystyle QD\) szakaszok hosszai összegének. A továbbiakban ezek minimumát kell megvizsgálni. Erre többféle változatot is ismertetünk.

1. változat. Legyen \(\displaystyle BP=x\), \(\displaystyle QD=y\), \(\displaystyle PQ=x+y=c\). Az \(\displaystyle APQ\) háromszög területe \(\displaystyle \frac{c}{2}\), mivel az \(\displaystyle A\)-hoz tartozó magasság egységnyi. Az \(\displaystyle ABPQD\) ötszög \(\displaystyle c\) területe ennek kétszerese, így a \(\displaystyle PCQ\) háromszög területe \(\displaystyle \frac{1}{2}(1-x)(1-y)=1-c\). A \(\displaystyle c\) minimumát fogjuk meghatározni. A számtani és mértani közép közötti egyenlőtlenség négyzetre emelt alakja alapján:

\(\displaystyle (1-x)(1-y)\le \left(\frac{1-x+1-y}{2}\right)^2.\)

Az eddigi eredményeink felhasználásával az egyenlőtlenség átírható olyan alakra, hogy abban csak a \(\displaystyle c\) szerepeljen ismeretlenként:

\(\displaystyle 2(1-c)\le \left(\frac{2-(x+y)}{2}\right)^2=\left(\frac{2-c}{2}\right)^2,\)

\(\displaystyle 8-8c\le 4-4c+c^2,\)

\(\displaystyle 8\le (c+2)^2,\)

\(\displaystyle 4\sqrt{2}-4\le 2c.\)

Itt \(\displaystyle 2c\) a töröttvonal hossza, ennek minimuma tehát \(\displaystyle 4\sqrt{2}-4\), akkor és csak akkor, ha \(\displaystyle x=y\).

2. változat. A \(\displaystyle PCQ\) derékszögű háromszög oldalai \(\displaystyle CP=1-x\), \(\displaystyle CQ=1-y\) és \(\displaystyle PQ=x+y\); a beírt kör sugara \(\displaystyle \varrho=\dfrac{CP+CQ-PQ}{2}=1-x-y\).

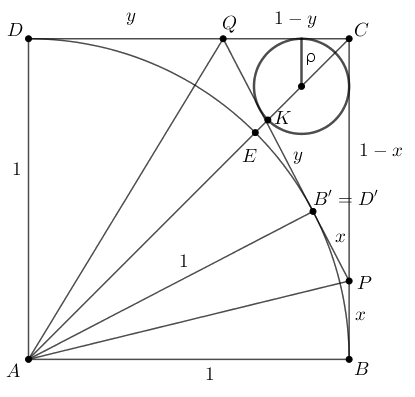
Mint az ábráról leolvasható:

és egyenlőség akkor áll fenn, ha \(\displaystyle E=K=B'=D'\). Tehát

\(\displaystyle \min(BP+PQ+QD) = 2\min(x+y) =4\big(\sqrt2-1\big). \)

3. változat. A négyzet oldala egységnyi, így \(\displaystyle BP=\text{tg}\,\alpha\), \(\displaystyle QD=\text{tg}\,\beta\).

\(\displaystyle \text{tg}\,\alpha+\text{tg}\,\beta=\frac{\sin \alpha}{\cos \alpha}+\frac{\sin \beta}{\cos \beta}=\frac{\sin \alpha \cdot \cos \beta + \sin \beta \cdot \cos \alpha}{\cos \alpha \cdot \cos \beta}=\frac{\sin(\alpha+\beta)}{\cos \alpha \cdot \cos \beta}.\)

Az \(\displaystyle \alpha\) és \(\displaystyle \beta\) szögek összege \(\displaystyle 45^\circ\), a tört számlálója állandó. A tört akkor lesz minimális, ha a nevezője maximális. Bővítsük a törtet \(\displaystyle 2\)-vel és a nevezőben alkalmazzunk addíciós tételt:

\(\displaystyle \frac{\sin(\alpha+\beta)}{\cos \alpha \cdot \cos \beta}=\frac{2\cdot \sin 45^\circ}{2\cdot \cos \alpha \cdot \cos \beta}=\frac{\sqrt{2}}{\cos(\alpha+\beta)+\cos(\alpha-\beta)}.\)

A nevezőben szereplő összeg első tagja \(\displaystyle \frac{\sqrt{2}}{2}\), a második pedig legfeljebb 1. A hosszak összege tehát akkor lesz minimális, ha \(\displaystyle \alpha=\beta=22,5^\circ\), a \(\displaystyle P\) és \(\displaystyle Q\) pontok az \(\displaystyle AC\) átlóra szimmetrikusan helyezkednek el.

4. változat. Jelöljük az \(\displaystyle \alpha\) szög tangensét \(\displaystyle x\)-szel, a \(\displaystyle \beta\) szög tangensét \(\displaystyle y\)-nal. A szögek összegének tangensére vonatkozó addíciós tétel szerint

\(\displaystyle 1=\text{tg}\,45^\circ=\text{tg}\, (\alpha+\beta)=\frac{x+y}{1-xy}.\)

Ezt – kicsit átrendezve – \(\displaystyle xy=1-(x+y)\) alakban fogjuk felhasználni.

Most tekintsük a számtani és mértani közép közötti egyenlőtlenség négyzetes alakját:

\(\displaystyle xy\le \left(\frac{x+y}{2}\right)^2,\)

illetve a szorzatot helyettesítve és \(\displaystyle (x+y)\) helyett új \(\displaystyle z\) ismeretlent bevezetve és az eddigiek alapján tudva, hogy \(\displaystyle z>0\):

\(\displaystyle 1-z\le \frac{z^2}{4},\)

\(\displaystyle 4\le z^2+4z,\)

\(\displaystyle 8\le z^2+4z+4=(z+2)^2,\)

\(\displaystyle 2\sqrt{2}-2\le z.\)

A feladatban szereplő töröttvonal hossza legalább ennek a duplája lesz. Egyenlőség akkor és csak akkor, ha \(\displaystyle x=y\).

5. változat. Ismét \(\displaystyle \text{tg}\, \alpha +\text{tg}\,\beta\) minimumát keressük. Az \(\displaystyle \alpha\) és \(\displaystyle \beta\) hegyes szögek összege \(\displaystyle 45^\circ\). Ebben a tartományban a tangensfüggvény szigorúan konvex, így

\(\displaystyle \frac{1}{2}\left(\text{tg}\, \alpha +\text{tg}\, \beta \right)\ge \text{tg}\,\frac{\alpha +\beta}{2}=\text{tg}\, 22,5^\circ.\)

A szigorú konvexitás alapján egyenlőség csak \(\displaystyle \alpha=\beta=22,5^\circ\) esetén.

A második és harmadik változatnál konkréten ki is számoltuk a töröttvonal hosszának minimumát: \(\displaystyle 4\sqrt{2}-4\).

Statisztika:

72 dolgozat érkezett.
4 pontot kapott:	54 versenyző.
3 pontot kapott:	11 versenyző.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2022. februári matematika feladatai