A B. 5237. feladat (2022. március)

B. 5237. Egy háromszögben \(\displaystyle r\) a beírt kör sugarát, \(\displaystyle R\) a köré írt kör sugarát, \(\displaystyle s\) pedig a háromszög félkerületét jelöli. Mutassuk meg, hogy ha \(\displaystyle r+2R=s\), akkor a háromszög derékszögű.

Javasolta: Fridrik Richárd Szeged)

(6 pont)

A beküldési határidő 2022. április 11-én LEJÁRT.

Megoldás. Használjuk a szokásos jelöléseket, legyenek a csúcsokból a beírt körhöz húzott érintőszakaszok \(\displaystyle x=s-a\), \(\displaystyle y=s-b\) és \(\displaystyle z=s-c\). Ekkor \(\displaystyle s=x+y+z\), valamint a jól ismert Héron-képlet a \(\displaystyle T=\sqrt{xyz(x+y+z)}\) alakot ölti. Felhasználjuk még az

\(\displaystyle r=\frac{T}{s}=\sqrt{\frac{xyz}{x+y+z}} \quad \text{és} \quad R=\frac{abc}{4T}=\frac{(x+y)(x+z)(y+z)}{4rs}\)

összefüggéseket (többféle alakjukban).

Először egy segédállítást igazolunk.

Segédállítás.

\(\displaystyle r(xy+xz+yz)-xyz=r^3-r^2s+4Rr^2.\)

Ennek igazolásához szorozzuk meg az állítás mindkét oldalát \(\displaystyle s\)-sel:

\(\displaystyle rs(xy+xz+yz)-xyzs=r^3s-r^2s^2+r\cdot4rRs.\)

Ebbe beírva a fentiekből azonnal következő \(\displaystyle 4rRs=(x+y)(x+z)(y+z)\) összefüggést:

\(\displaystyle T(xy+xz+yz)-T^2=r^2T-T^2+\frac{T}{s}\cdot (x+y)(x+z)(y+z).\)

Mindkét oldalhoz \(\displaystyle T^2\)-t adva, majd \(\displaystyle T\)-vel osztva:

\(\displaystyle xy+xz+yz=\frac{xyz}{x+y+z}+\frac{(x+y)(x+z)(y+z)}{x+y+z}.\)

Ez átszorzással és a zárójelek felbontásával könnyen ellenőrizhető azonosság, s mivel ekvivalens átalakításokat végeztünk, így a segédállítást beláttuk.

Most számítsuk ki a segédállítás segítségével az \(\displaystyle (r-x)(r-y)(r-z)\) szorzatot:

\(\displaystyle (r-x)(r-y)(r-z)=r^3-r^2(x+y+z)+r(xy+xz+yz)-xyz=r^3-r^2s+r^3-r^2s+4Rr^2=2r^2(r+2R-s)=0\)

a feltétel szerint. Mivel \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) szerepe szimmetrikus, így feltehető, hogy \(\displaystyle r-x=0\), azaz \(\displaystyle r=x\).

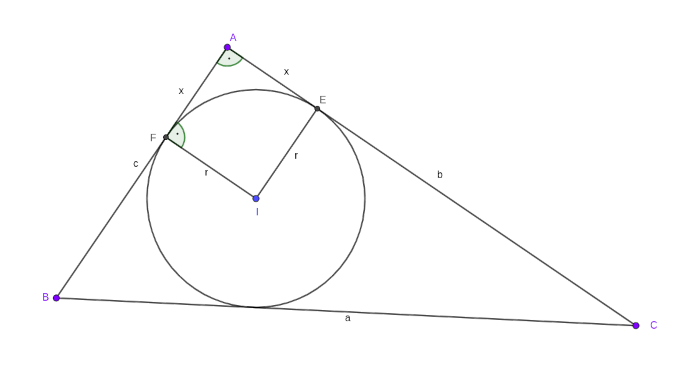
Így az ábrán lévő \(\displaystyle AFIE\) négyszög derékszögű rombusz, azaz négyzet, ami miatt az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-nál levő szöge derékszög. Ezzel az állítást beláttuk.

Megjegyzés. A megoldásban az \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) érintőszakaszok segítségével kifejeztük az \(\displaystyle r\), \(\displaystyle R\) és \(\displaystyle s\) adatokat. Ezeket visszaírva a feltételbe rendezés, négyzetreemelés majd nullára rendezés után egy hatodfokú, háromváltozós, homogén polinomot kapunk. Direkt számolással ellenőrizhető, hogy ez a polinom \(\displaystyle (x^2+xy+xz-yz)(y^2+xy+yz-xz)(z^2+xz+yz-xy)\) szorzatalakban írható. Szintén direkt számolás mutatja, hogy

\(\displaystyle (x^2+xy+xz-yz)(y^2+xy+yz-xz)(z^2+xz+yz-xy)=\frac{(a^2+b^2-c^2)(a^2+c^2-b^2)(b^2+c^2-a^2)}{8}.\)

Ezekből és a Pitagorasz-tétel megfordításából az állítás következik.

Statisztika:

33 dolgozat érkezett.
6 pontot kapott:	Bényei Borisz, Chrobák Gergő, Diaconescu Tashi, Duchon Márton, Fülöp Csilla, Horváth 530 Mihály, Jánosik Máté, Koleszár Domonkos, Lovas Márton, Mohay Lili Veronika, Nagy 551 Levente, Németh Márton, Romaniuc Albert-Iulian, Simon László Bence, Somogyi Dalma, Tarján Bernát, Tran Dávid, Varga Boldizsár, Veres Dorottya, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
5 pontot kapott:	Bencsik Dávid, Csonka Illés, Kalocsai Zoltán.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2022. márciusi matematika feladatai