 |
A B. 5243. feladat (2022. április) |
B. 5243. Az \(\displaystyle ABC\) háromszögben \(\displaystyle CAB\sphericalangle=48^{\circ}\) és \(\displaystyle ABC\sphericalangle=54^{\circ}\). A háromszög egy belső \(\displaystyle D\) pontjára teljesül, hogy \(\displaystyle CDB\sphericalangle=132^{\circ}\) és \(\displaystyle BCD\sphericalangle=30^{\circ}\). Igazoljuk, hogy az \(\displaystyle ACDB\) töröttvonalat alkotó szakaszokból nem szerkeszthető háromszög.
(5 pont)
A beküldési határidő 2022. május 10-én LEJÁRT.
I. megoldás. Megmutatjuk, hogy \(\displaystyle AC=CD+DB\), azaz a szakaszokra nem teljesül a háromszög egyenlőtlenség. Feltehetjük, hogy \(\displaystyle BC=1\), valamint vegyük észre, hogy az \(\displaystyle ABC\) és \(\displaystyle BCD\) háromszögek szögei adottak.
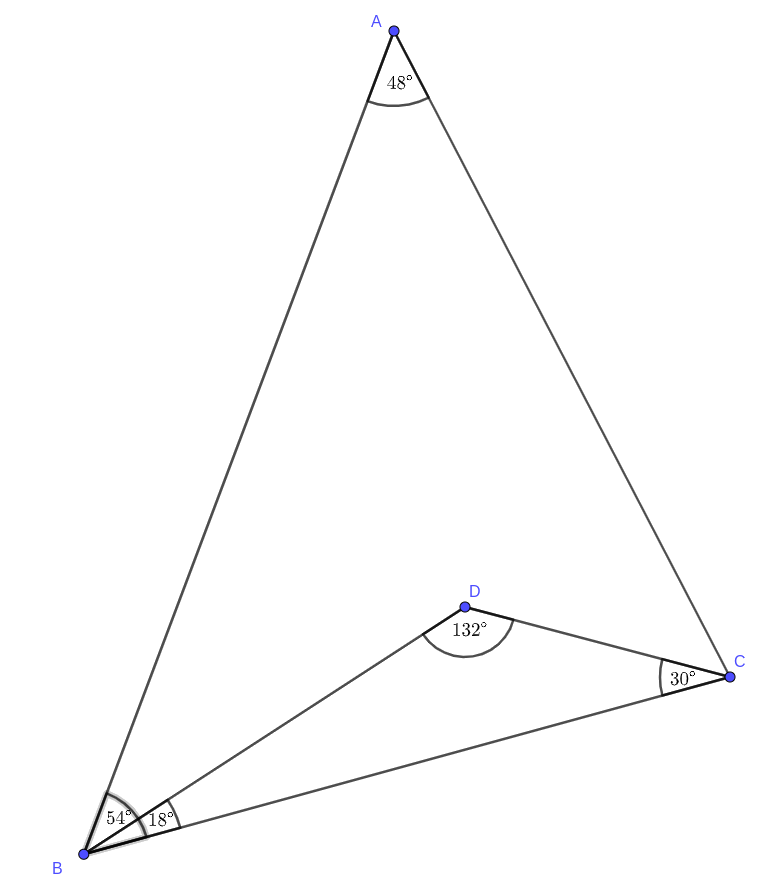
Felírva a szinusz-tételt az \(\displaystyle ABC\) és a \(\displaystyle BCD\) háromszögekben:
\(\displaystyle \frac{CB}{\sin 48^\circ}=\frac{AC}{\sin 54^\circ} \qquad\text{és} \qquad \frac{CB}{\sin 132^\circ}=\frac{CD}{\sin 18^\circ}=\frac{BD}{\sin 30^\circ}.\)
Ezekből, kihasználva, hogy \(\displaystyle CD=1\) és \(\displaystyle \sin 132^\circ=\sin 48^\circ\) kapjuk, hogy
\(\displaystyle AC=\frac{\sin 54^\circ}{\sin 48^\circ}\, , \, CD=\frac{\sin 18^\circ}{\sin 48^\circ}\; \text{és} \; BD=\frac{\sin 30^\circ}{\sin 48^\circ}.\)
Vagyis elegendő megmutatnunk, hogy \(\displaystyle \sin 54^\circ=\sin 30^\circ+\sin 18^\circ=1/2+\sin 18^\circ\). Ehhez rajzoljunk egy \(\displaystyle XYZ\) egyenlő szárú háromszöget, amelynek \(\displaystyle XY\) alapja egységnyi, szárszöge \(\displaystyle 36^\circ\).
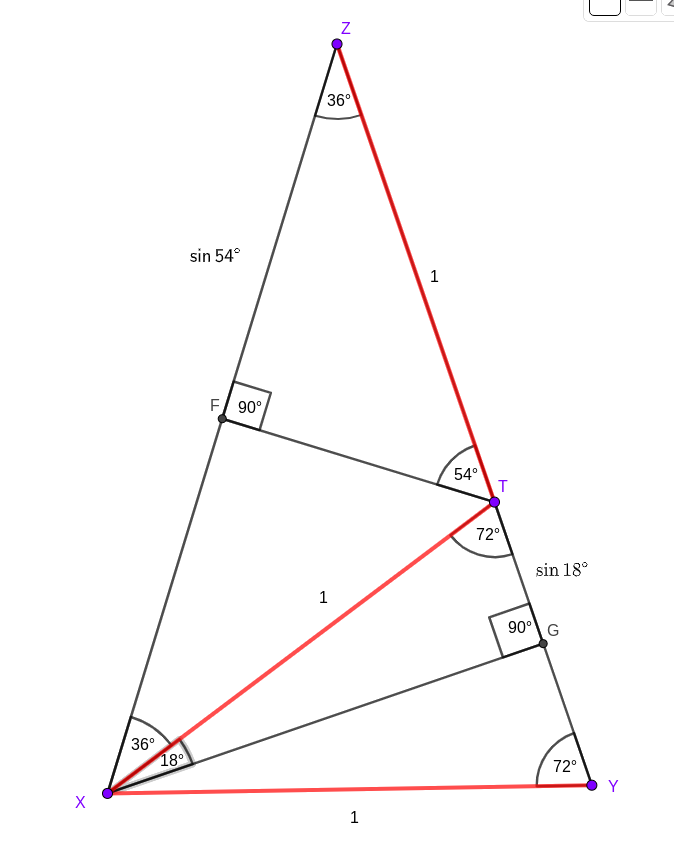
Az \(\displaystyle XT\) belső szögfelező a háromszöget két egyenlő szárú háromszögre bontja az ábra szerint. Az \(\displaystyle XTZ\) háromszögből leolvasható, hogy \(\displaystyle XZ=2\sin 54^\circ\), míg az \(\displaystyle XYT\) háromszögből \(\displaystyle YZ=YT+TZ=2\sin 18^\circ +1\). Ezekből \(\displaystyle \sin 54^\circ=1/2+\sin 18^\circ\) azonnal következik, és a bizonyítást befejeztük.
II. megoldás Az ábrát belerajzoljuk egy szabályos hatvanszögbe. Legyen \(\displaystyle P_1P_2\ldots P_{60}\) szabályos hatvanszög, a középpontja \(\displaystyle O\). A különböző átlók közötti szögeket a kerületi szögek tételéből számolhatjuk: a \(\displaystyle P_iP_j\) és \(\displaystyle P_kP_\ell\) egyenesek előjeles szöge \(\displaystyle (k+\ell-i-j)\cdot 3^\circ\pmod{180^\circ}\).
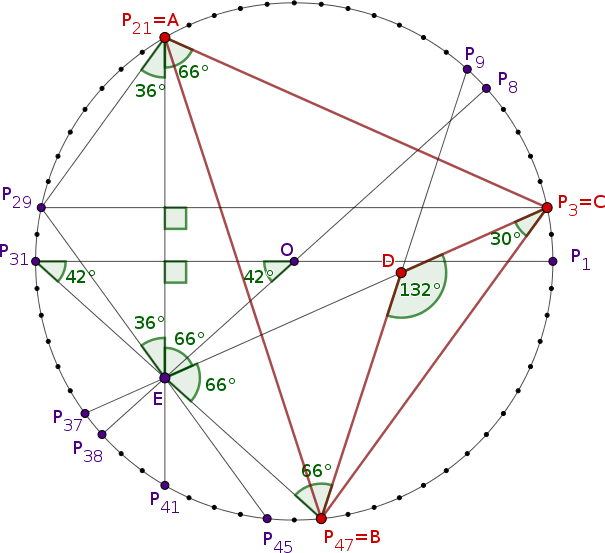
Arra lesz szükségünk, hogy a \(\displaystyle P_3P_{37}\), a \(\displaystyle P_{21}P_{41}\) és a \(\displaystyle P_{31}P_{47}\) átló egy ponton megy át. Legyen \(\displaystyle E=P_{21}P_{41}\cap P_8P_{38}\). Az \(\displaystyle OP_{21}P_{31}\) és \(\displaystyle OP_{31}P_{41}\) háromszögek szabályosak, ezért a \(\displaystyle P_{21}P_{41}\) átló az \(\displaystyle OP_{31}\) sugár felező merőlegese. Az \(\displaystyle OP_{38}\) egyenes tükörképe a \(\displaystyle P_{21}P_{41}\)-re \(\displaystyle P_{31}P_{47}\), ezért \(\displaystyle P_{31}P_{47}\) is átmegy \(\displaystyle E\)-n. A \(\displaystyle P_{31}P_{47}\) tükörképe a \(\displaystyle P_8P_{38}\) átmérőre \(\displaystyle P_{29}P_{45}\), ez is átmegy \(\displaystyle E\)-n. Végül vegyük észre, hogy a \(\displaystyle P_3P_{21}P_{29}E\) négyszög átlói merőlegesek, mert \(\displaystyle P_3P_{29}\parallel P_1P_{31}\perp P_{21}P_{41}\), és a \(\displaystyle P_{21}P_{31}E\) háromszög egyenlő szárú, mert \(\displaystyle EP_{21}P_{29}\sphericalangle= P_{29}EP_{21}\sphericalangle =36^\circ\). A \(\displaystyle P_3P_{21}P_{29}E\) négyszög tehát deltoid, ezért a \(\displaystyle P_3P_{21}\) egyenesnek a \(\displaystyle P_3P_{29}\)-re való tükörképe, a \(\displaystyle P_3P_{37}\) átló is átmegy \(\displaystyle E\)-n.
Legyen ezek után \(\displaystyle A=P_{21}\), \(\displaystyle B=P_{47}\), \(\displaystyle C=P_3\) és \(\displaystyle D=BP_9\cap CP_{37}\), ekkor megkapjuk a feladatbeli elrendezést. Az \(\displaystyle AEC\) és az \(\displaystyle EBD\) háromszögek egyenlő szárúak, így \(\displaystyle CA=CE\), illetve \(\displaystyle DE=DB\); emiatt
\(\displaystyle BD+DC=ED+DC=EC=AC. \)
A \(\displaystyle BD\), \(\displaystyle DC\) és \(\displaystyle AC\) aszakaszokra nem teljesül a háromszög-egyenlőtlenség.
Statisztika:
53 dolgozat érkezett. 5 pontot kapott: Bencsik Dávid, Bencz Benedek, Bényei Borisz, Christ Miranda Anna, Chrobák Gergő, Csilling Dániel, Diaconescu Tashi, Duchon Márton, Erdélyi Kata, Farkas 005 Bendegúz, Farkas 512 Izabella, Fülöp Csilla, Horváth 530 Mihály, Kalocsai Zoltán, Koleszár Domonkos, Kosztolányi Karina, Kovács Benedek Noel, Kurucz Kitti, Lovas Márton, Melján Dávid Gergő, Mohay Lili Veronika, Móricz Benjámin, Nádor Artúr, Nagy 429 Leila, Németh Márton, Nguyen Kim Dorka, Pintér Benedek, Romaniuc Albert-Iulian, Schneider Dávid, Seprődi Barnabás Bendegúz, Simon László Bence, Sipeki Márton, Somogyi Dalma, Szabó Enikő Lilla, Szakács Ábel, Tarján Bernát, Török Eszter Júlia, Tran Dávid, Varga Boldizsár, Vincze Farkas Csongor, Wiener Anna, Zömbik Barnabás. 4 pontot kapott: Csonka Illés, Diószeghy Erzsébet, Mészáros Anna Veronika, Op Den Kelder Ábel, Ottrok Barbara, Szakács Domonkos, Virág Rudolf. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2022. áprilisi matematika feladatai

