 |
A B. 5255. feladat (2022. szeptember) |
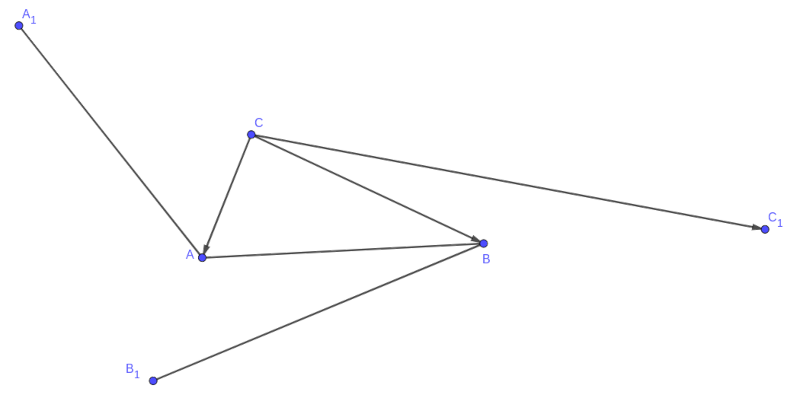
B. 5255. Tükrözzük középpontosan az \(\displaystyle ABC\) háromszög \(\displaystyle A\) csúcsát \(\displaystyle B\)-re, \(\displaystyle B\) csúcsát \(\displaystyle C\)-re, és \(\displaystyle C\) csúcsát \(\displaystyle A\)-ra, így kapjuk rendre a \(\displaystyle C_1\), \(\displaystyle A_1\) és \(\displaystyle B_1\) pontokat. Mutassuk meg, hogy \(\displaystyle AA_1\), \(\displaystyle BB_1\) és \(\displaystyle CC_1\) hosszúságú oldalakkal háromszög szerkeszthető.
(3 pont)
A beküldési határidő 2022. október 10-én LEJÁRT.
Megoldás. A felezőpontra ismert formula szerint \(\displaystyle \overrightarrow{CB}=(\overrightarrow{CA}+\overrightarrow{CC_1})/2\), amiből \(\displaystyle \overrightarrow{CC_1}=2\overrightarrow{CB}-\overrightarrow{CA}\). Hasonlóan láthatjuk, hogy \(\displaystyle \overrightarrow{BB_1}=2\overrightarrow{BA}-\overrightarrow{BC}\) és \(\displaystyle \overrightarrow{AA_1}=2\overrightarrow{AC}-\overrightarrow{AB}\). Ezeket összeadva
\(\displaystyle \overrightarrow{AA_1}+\overrightarrow{BB_1}+\overrightarrow{CC_1}=(2\overrightarrow{CB}-\overrightarrow{CA})+(2\overrightarrow{BA}-\overrightarrow{BC})+(2\overrightarrow{AC}-\overrightarrow{AB}) =3(\overrightarrow{BA}+\overrightarrow{CB}+\overrightarrow{AC})=\mathbf 0.\)
Továbbá vegyük észre, hogy \(\displaystyle \overrightarrow{AA_1}+4\overrightarrow{BB_1}-2\overrightarrow{CC_1}=2\overrightarrow{AC}-\overrightarrow{AB}+8\overrightarrow{BA}-4\overrightarrow{BC}-4\overrightarrow{CB}+2\overrightarrow{CA}=9\overrightarrow{BA}.\) Hasonlóan, \(\displaystyle \overrightarrow{BB_1}+4\overrightarrow{CC_1}-2\overrightarrow{AA_1}=9\overrightarrow{CB}\) és \(\displaystyle \overrightarrow{CC_1}+4\overrightarrow{AA_1}-2\overrightarrow{BB_1}=9\overrightarrow{AC}\). Így \(\displaystyle \overrightarrow{AA_1}\), \(\displaystyle \overrightarrow{BB_1}\) és \(\displaystyle \overrightarrow{CC_1}\) vektorok nem lehetnek egymással párhuzamosak, mert akkor \(\displaystyle ABC\) oldalvektorai is párhuzamosak lennének.
Így \(\displaystyle \overrightarrow{AA_1}\), \(\displaystyle \overrightarrow{BB_1}\) és \(\displaystyle \overrightarrow{CC_1}\) egy nem elfajuló háromszög oldalvektorai, amiből az állítás azonnal következik.
Megjegyzés. Negatív osztási arányt is értelmezve az osztópontba mutató vektorra vonatkozó ismert formula általánosítható arra az esetre, ha az osztópont nem belső pontja a pontok által meghatározott szakasznak, de illeszkedik az egyenesükre. Tulajdonképpen ezt használtuk a megoldásban.
Statisztika:
191 dolgozat érkezett. 3 pontot kapott: 94 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 62 versenyző. Nem versenyszerű: 6 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2022. szeptemberi matematika feladatai

