 |
A B. 5265. feladat (2022. október) |
B. 5265. Nagyítsuk kétszeresére egy derékszögű háromszög beírt körét a derékszögű csúcsból. Mutassuk meg, hogy a kapott kör érinti a háromszög körülírt körét.
Javasolta: Vígh Viktor (Szeged)
(4 pont)
A beküldési határidő 2022. november 10-én LEJÁRT.
1. megoldás A kompakt leírás kedvéért helyezzük el a derékszögű háromszöget a derékszögű koordinátarendszerben úgy, hogy \(\displaystyle C\) derékszögű csúcsa az origóba essen, továbbá \(\displaystyle A(a,0)\) és \(\displaystyle B(0,b)\), ahol \(\displaystyle a,b>0\) a háromszög befogói. Használjuk az ábra jelöléseit!
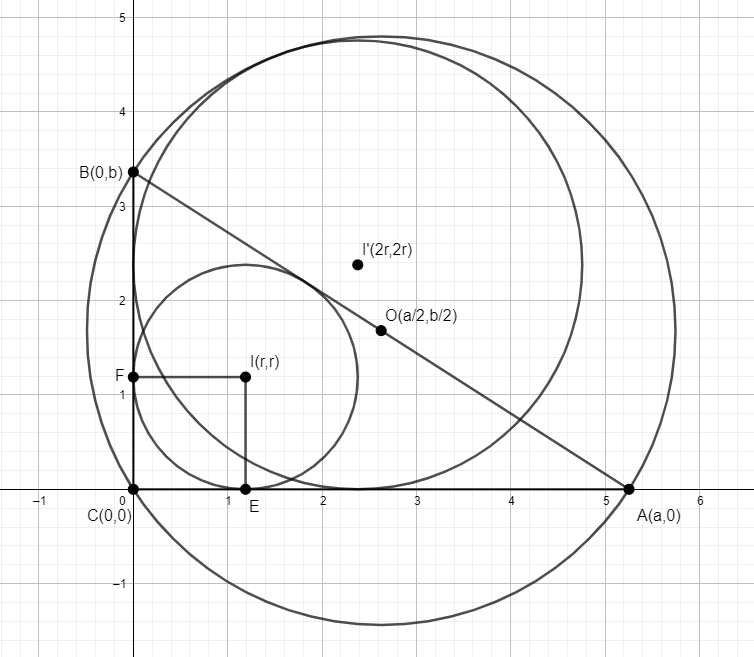
A \(\displaystyle CEIF\) négyszög egyszerre deltoid és téglalap, ezért négyzet. Oldala egyrészről a beírt kör \(\displaystyle r\) sugara, másrészről a \(\displaystyle C\) csúcsból a beírt körhöz húzott érintőszakasz \(\displaystyle z\), amelyről jól ismert, hogy \(\displaystyle z=s-c=(a+b-c)/2\). Ebből következik, hogy \(\displaystyle r=(a+b-c)/2\), valamint az \(\displaystyle I\) pont koordinátáit is megkaptuk. Világos, hogy a kétszeres nagyítás után kapott kör sugarára \(\displaystyle r'=2r=a+b-c\), középontjára \(\displaystyle I'(a+b-c,a+b-c)\) teljesül.
Az \(\displaystyle ABC\) háromszög körülírt körének középpontja az átfogó felezőpontja, azaz az \(\displaystyle O(a/2,b/2)\) pont, sugara pedig az átfogó fele, \(\displaystyle R=c/2\). A feladat állítása következik, ha megmutatjuk, hogy \(\displaystyle R=r'+OI'\), amivel ekvivalens \(\displaystyle OI'^2=(R-r')^2\). (A sugáregyenlőtlenség szerint \(\displaystyle r'<R\).)
\(\displaystyle OI'^2\) felírható a Pitagorasz-tétel (vagy ha úgy tetszik, a távolságformula) segítségével:
\(\displaystyle OI'^2=\left ((a+b-c)-\frac a2\right )^2+\left ((a+b-c)-\frac b2 \right)^2.\)
Elegendő tehát belátnunk, hogy
\(\displaystyle \left ((a+b-c)-\frac a2\right )^2+\left ((a+b-c)-\frac b2 \right)^2=\left (\frac c2-(a+b-c)\right )^2.\)
A négyzetreemeléseket elvégezve, és a Pitagorasz-tételt az \(\displaystyle ABC\) háromszögre felhasználva ez könnyen ellenőrizhető, hogy teljesül. Ezzel az állítást beláttuk.
2. megoldás A derékszögű háromszög magasságpontja a háromszög derékszögű csúcsa. Ismert, hogy a magasságpontból a körülírt kört felére kicsinyítve a háromszög Feuerbach-körét kapjuk. A Feuerbach-tétel szerint a Feuerbach-kör érinti a beírt kört, amiből a feladat állítása azonnal következik.
Statisztika:
95 dolgozat érkezett. 4 pontot kapott: 72 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2022. októberi matematika feladatai

