 |
A B. 5268. feladat (2022. október) |
B. 5268. Az \(\displaystyle ABC\) háromszög beírt körének középpontját jelölje \(\displaystyle I\). Az \(\displaystyle ABC\) háromszög belsejében, az \(\displaystyle ABI\) körön vegyünk fel egy \(\displaystyle P\) pontot. Az \(\displaystyle AP\) egyenes \(\displaystyle AI\)-re vett tükörképe az \(\displaystyle ABI\) kört az \(\displaystyle A\)-n kívül még a \(\displaystyle Q\) pontban metszi. Bizonyítsuk be, hogy \(\displaystyle CP=CQ\).
Javasolta: Kocsis Szilveszter (Budapest)
(6 pont)
A beküldési határidő 2022. november 10-én LEJÁRT.
Megoldás. Közismert, hogy \(\displaystyle I\)-n (a beírt kör középpontján) átmegy mindhárom belső szögfelező, ezeket tehát mindenképp érdemes megrajzolnunk. Rajzoljuk meg a külső szögfelezőket is, később majd ezeknek is jut hasznos szerep. Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) csúcsokhoz tartozó belső és külső szögfelezőt jelölje rendre \(\displaystyle f_A\) és \(\displaystyle g_A\), \(\displaystyle f_B\) és \(\displaystyle g_B\), illetve \(\displaystyle f_C\) és \(\displaystyle g_C\).
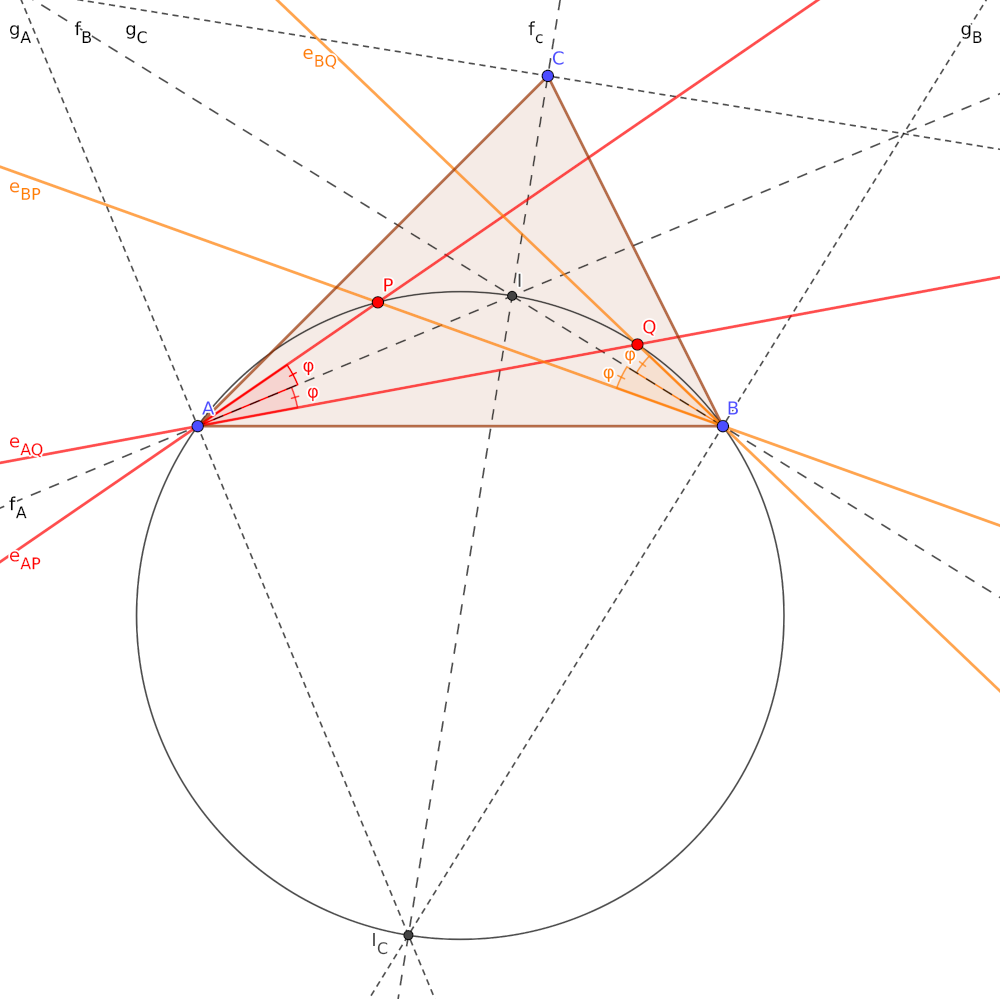
Legyen \(\displaystyle IAP \sphericalangle = \varphi\), ekkor a tükrözés miatt persze \(\displaystyle QAI \sphericalangle\) is \(\displaystyle \varphi\). (Mivel \(\displaystyle AP\), és így az \(\displaystyle AQ\) félegyenes a \(\displaystyle BAC\) szögtartományon belül halad, ezért \(\displaystyle P\)-hez hasonlóan \(\displaystyle Q\) is az \(\displaystyle ABI\) kör \(\displaystyle I\)-t tartalmazó ívén lesz.) A kerületi szögek tétele miatt ekkor \(\displaystyle IBP \sphericalangle = IAP \sphericalangle = \varphi\) és \(\displaystyle QBI \sphericalangle = QAI \sphericalangle = \varphi\). Mivel
- az \(\displaystyle AP\) egyenesnek az \(\displaystyle f_B\) szögfelezőre vett tükörképe \(\displaystyle AQ\) (a feladat feltételei szerint),
- míg a \(\displaystyle BP\) egyenesnek az \(\displaystyle f_B\) szögfelezőre vett tükörképe \(\displaystyle BQ\) (a kiszámított szögek miatt),
ezért a \(\displaystyle P\) pontnak \(\displaystyle Q\) éppen az izogonális konjugáltja, azaz az \(\displaystyle e_{CP}\) egyenesnek az \(\displaystyle f_C\)-re vett tükörképe éppen az \(\displaystyle e_{CQ}\) egyenes, másképpen mondva \(\displaystyle PCI \sphericalangle = ICQ \sphericalangle\).
Motiváció a megoldás következő részéhez: Innentől a bizonyítandó állításunk (\(\displaystyle CP = CQ\)) akkor tud teljesülni, ha \(\displaystyle P\) és \(\displaystyle Q\) egymás tükörképei az \(\displaystyle f_C\) egyenesre nézve. Ennek elégséges (és szükséges) feltétele, hogy az \(\displaystyle ABP\) kör szimmetrikus legyen az \(\displaystyle f_C\) egyenesre. Hogyan láthatjuk be, hogy az \(\displaystyle ABP\) kör szimmetrikus az \(\displaystyle f_C\) egyenesre? Ehhez hasznos észrevennünk, hogy az \(\displaystyle ABI\) kör áthalad egy negyedik ,,híres'' ponton is.
Jelölje \(\displaystyle g_A\) és \(\displaystyle g_B\) metszéspontját (azaz a háromszög \(\displaystyle c\) oldalához tartozó hozzáírt körének középpontját) \(\displaystyle I_C\). Mivel a belső és külső szögfelezők merőlegesek egymásra, ezért \(\displaystyle II_C\) Thalész-köre átmegy \(\displaystyle A\) és \(\displaystyle B\) pontokon. Vagyis az \(\displaystyle ABP\) kör éppen megegyezik ezzel a Thalész-körrel. Az \(\displaystyle II_C\) átmérő éppen az \(\displaystyle f_C\) szögfelező része, tehát az \(\displaystyle ABI\) kör szimmetrikus az \(\displaystyle f_C\) szögfelezőre.
Következésképpen \(\displaystyle P\)-nek az \(\displaystyle f_C\) szögfelezőre vett tükörképe valóban \(\displaystyle Q\) (hiszen az \(\displaystyle e_{CP}\) egyenes tükörképe \(\displaystyle e_{CQ}\), míg a \(\displaystyle k_{ABI}\) kör tükörképe önmaga, márpedig \(\displaystyle P = e_{CP} \cap k_{ABI}\), míg \(\displaystyle q = e_{CQ} \cap k_{ABI}\)). Pont és tengelyes tükörképe egyforma távol van a tengely bármely pontjától, tehát \(\displaystyle CP = CQ\).
1. megjegyzés (az izogonális konjugálásról). Az izogonális konjugálás tétele a következőt mondja ki: legyen \(\displaystyle P\) az \(\displaystyle ABC\) háromszög síkjában egy tetszőleges olyan pont, amely nem esik rá \(\displaystyle ABC\) körülírt körére. Ha az \(\displaystyle AP\) egyenest tükrözzük az \(\displaystyle A\) csúcs belső szögfelezőjére, a \(\displaystyle BP\)-t a \(\displaystyle B\) belső szögfelezőjére, míg \(\displaystyle CP\)-t a \(\displaystyle C\) belső szögfelezőjére, akkor a kapott három egyenes egy ponton megy át. Ezt a metszéspontot nevezzük a \(\displaystyle P\) pont izogonális konjugáltjának.
Ez a tétel bizonyítható például Ceva tételének trigonometrikus alakjára való hivatkozással – részletekért ld. pl. Reiman István, Dobos Sándor: Nemzetközi Matematikai Diákolimpiák 1959–2003 (Typotex Kiadó, 2003) c. könyvében az 1996/2. feladathoz kapcsolódó [41] számú jegyzetét. Egy másik szép elemi geometriai indoklás olvasható Záhorský Ákos: Az izogonális konjugálás c. szakdolgozatában (ELTE Matematikus BSc 2021, szabadon elérhető elektronikusan: https://web.cs.elte.hu/blobs/diplomamunkak/bsc_mat/2021/zahorsky_akos.pdf). Ebben a szakdolgozatban az izogonális konjugálás számos érdekes és hasznos tulajdonságával is megismerkedhetnek az érdeklődők.
2. megjegyzés (a diszkusszióról). A feladat feltételei között szerepel, hogy \(\displaystyle P\) a háromszög belsejében szerepel – így a megoldás nem igényel diszkussziót. Valójában a \(\displaystyle P\) pontot választhattuk volna az \(\displaystyle APB\) körnek a háromszögön kívüli részén is. A bemutatott gondolatmenet kis változtatással továbbra is működne, pl. az \(\displaystyle IAP \sphericalangle = QAI \sphericalangle = IBP \sphericalangle = QBI \sphericalangle\) egyenlőség helyett, az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle I\), \(\displaystyle P\), \(\displaystyle Q\) pontok körön való sorrendjánek megváltozása miatt néha az \(\displaystyle IAP \sphericalangle = 180^{\circ} - QAI \sphericalangle = 180^{\circ} - IBP \sphericalangle = QBI \sphericalangle\) egyenlőség áll fenn.
Mivel \(\displaystyle P\) nem lehet a körülírt körön – hiszen az \(\displaystyle APB\) kör már két pontban (\(\displaystyle A\) és \(\displaystyle B\)) metszi a körülírt kört –, így a megoldás kulcsát jelentő izogonális konjugálás mindig működik.
Statisztika:
71 dolgozat érkezett. 6 pontot kapott: 52 versenyző. 5 pontot kapott: 4 versenyző. 4 pontot kapott: 4 versenyző. 3 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2022. októberi matematika feladatai
