 |
A B. 5271. feladat (2022. november) |
B. 5271. Legyen \(\displaystyle ABC\) olyan egyenlő szárú derékszögű háromszög, amelyben a \(\displaystyle C\) csúcsnál van a derékszög. Jelöljük ki az \(\displaystyle AB\) oldal belsejében az \(\displaystyle A'\), a \(\displaystyle BC\) oldal belsejében a \(\displaystyle B'\) és a \(\displaystyle CA\) oldal belsejében a \(\displaystyle C'\) pontokat úgy, hogy az \(\displaystyle A'B'C'\) háromszög hasonló legyen az \(\displaystyle ABC\) háromszöghöz.
Mutassuk meg, hogy az \(\displaystyle AB\) oldal felezőpontja, az \(\displaystyle A'B'\) szakasz felezőpontja és a \(\displaystyle C\) pont egy egyenesre esik.
Javasolta: Hajdu Endre (Sopron) és Hujter Mihály (Budapest)
(3 pont)
A beküldési határidő 2022. december 12-én LEJÁRT.
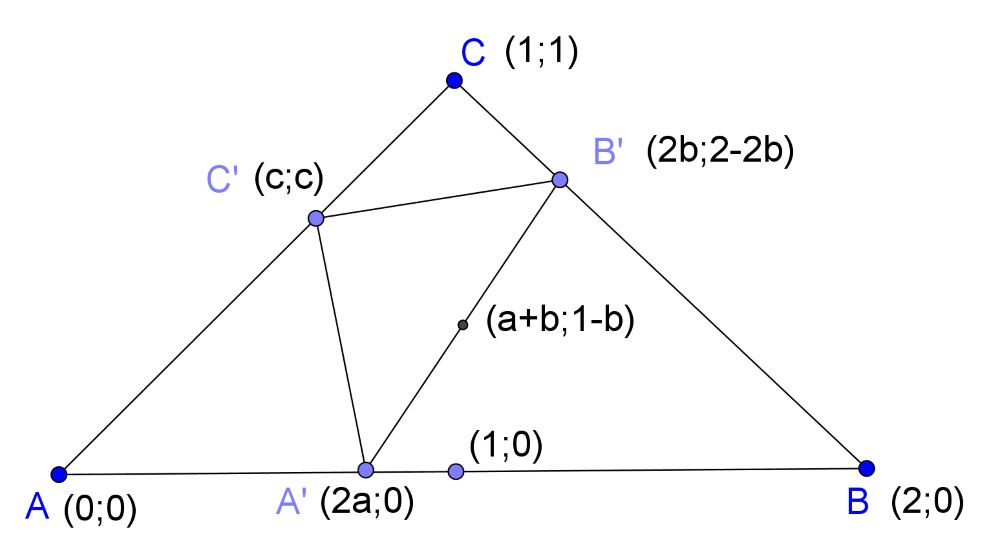
Megoldás. Helyezzük el a háromszöget a derékszögű koordináta-rendszerben úgy, hogy az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) csúcsok koordinátái rendre \(\displaystyle (0;0)\), \(\displaystyle (2;0)\), \(\displaystyle (1;1)\). Az illeszkedési feltételek miatt az \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) csúcsok koordinátái rendre \(\displaystyle (2a;0)\), \(\displaystyle (2b;2-2b)\), \(\displaystyle (c;c)\) alakban írhatóak alkalmas \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) valósakkal. Ekkor a \(\displaystyle \overrightarrow{C'A'}\) vektor koordinátái \(\displaystyle (2a-c;-c)\), a \(\displaystyle \overrightarrow{C'B'}\) vektor koordinátái pedig \(\displaystyle (2b-c;2-2b-c)\). Az \(\displaystyle AB\) szakasz felezőpontjának koordinátái \(\displaystyle (1;0)\), az \(\displaystyle A'B'\) szakasz felezőpontjának koordinátái pedig \(\displaystyle (a+b;1-b)\).
Az \(\displaystyle A'B'C'\) háromszög pontosan akkor hasonló \(\displaystyle ABC\)-hez (az azonos betűzésnek megfelelően), ha a \(\displaystyle C'\) pont körüli \(\displaystyle +90^{\circ}\)os elforgatás a \(\displaystyle \overrightarrow{C'A'}\) vektort \(\displaystyle \overrightarrow{C'B'}\)-be viszi, azaz ha
\(\displaystyle (c;2a-c) = (2b-c;2-2b-c)\,. \)
Innen, a második koordináták egyenlősége alapján \(\displaystyle 2a-c = 2-2b-c\), azaz \(\displaystyle a+b\)=1. Tehát \(\displaystyle C\), valamint az \(\displaystyle A'B'\) és az \(\displaystyle AB\) szakaszok felezőpontja egyaránt illeszkedik az \(\displaystyle x=1\) egyenletű egyenesre.
Statisztika:
104 dolgozat érkezett. 3 pontot kapott: 51 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 24 versenyző. 0 pontot kapott: 13 versenyző. Nem versenyszerű: 2 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2022. novemberi matematika feladatai
