Problem B. 5285. (December 2022)

B. 5285. In an acute-angled triangle \(\displaystyle ABC\), \(\displaystyle AB=AC\). Points \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\) are moving along the circumscribed circle of the triangle, so that triangle \(\displaystyle A'B'C'\) always remain congruent to triangle \(\displaystyle ABC\), and have the same orientation. Let \(\displaystyle P\) be the intersection of lines \(\displaystyle BB'\) and \(\displaystyle CC'\). Show that the lines \(\displaystyle A'P\) all pass through a certain point.

Proposed by G. Kós, Budapest

(6 pont)

Deadline expired on January 10, 2023.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. A megoldás elolvasása előtt mindenképp javasoljuk Kiss Géza: Komplex számokkal elengánsabb c. cikkének áttanulmányozását, illetve a komplex számokat nem ismerőknek Surányi János: Ismerkedés a komplex számokkal c. háromrészes cikksorozatát a KöMaL 1948. évi számaiból.

Koordinátázzuk meg a síkot a komplex számokkal a szokásos módon, az egyszerűség kedvéért a pontokat és az őket koordinátázó komplex számot ugyanazzal a nagybetűvel jelöljük. Feltehetjük, hogy az \(\displaystyle ABC\triangle\) körülírt körének középpontja az origó, továbbá \(\displaystyle A=1\). Bevezetjük a \(\displaystyle \varphi\) argumentumú, egységnyi abszolút értékű komplex számra az \(\displaystyle u(\varphi)=\cos \varphi + i \sin \varphi\) jelölést. Ekkor a szimmetria miatt \(\displaystyle B=u(\omega)\) és \(\displaystyle C=u(-\omega)\) alkalmas \(\displaystyle \omega\) valóssal.

A feltételek szerint az \(\displaystyle A'B'C'\triangle\)-et az \(\displaystyle ABC\) háromszög alkalmas elforgatásával kapjuk, legyen a forgatás szöge \(\displaystyle \varphi\). Ekkor a trigonometrikus alakban való szorzás szabálya miatt \(\displaystyle A'=A\cdot u(\varphi)=u(\varphi)\), \(\displaystyle B'=B\cdot u(\varphi)=u(\varphi+\omega)\) és \(\displaystyle C'=C\cdot u(\varphi)=u(\varphi-\omega)\) szintén csupa egységnyi komplex számok.

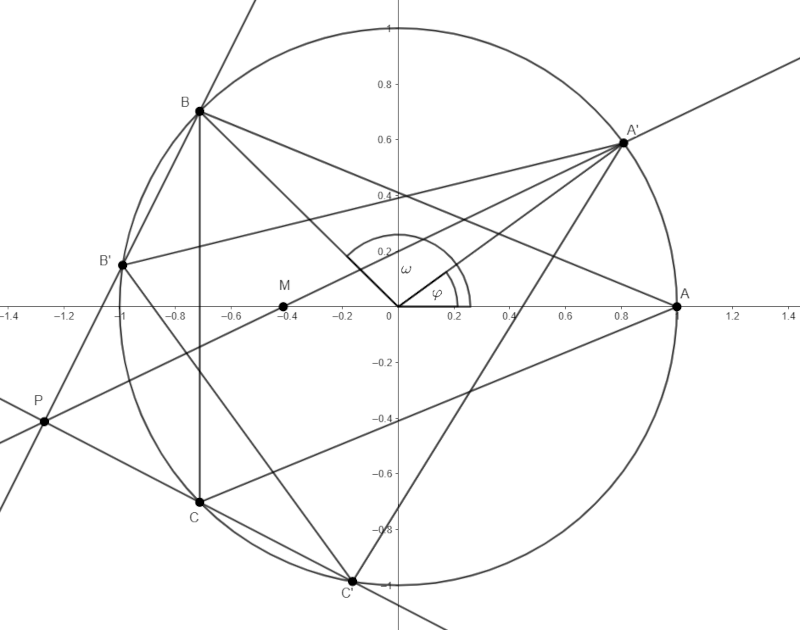
A \(\displaystyle BB'\) és \(\displaystyle CC'\) egyenesek metszéspontja felírható az ismert formulával:

A beszorzás után felhasználjuk a \(\displaystyle BC=1\) azonosságot, valamint az ebből adódó \(\displaystyle B'C^2=u(\varphi)BC^2=u(\varphi)C=C'\) és \(\displaystyle C'B^2=u(\varphi)CB^2=u(\varphi)B=B'\) összefüggéseket, így kapjuk, hogy:

Itt vegyük észre, hogy \(\displaystyle B+C=(\cos \omega+ i\sin \omega)+(\cos (-\omega)+ i\sin(- \omega))=2\cos \omega\) egy valós szám. Továbbá \(\displaystyle 2\cos (\varphi/2) u(\varphi/2)=2\cos (\varphi/2) (\cos (\varphi/2))+i\sin(\varphi/2))=2\cos^2 (\varphi/2)+i2\sin(\varphi/2)\cos(\varphi/2)=1+\cos\varphi+i\sin \varphi=1+u(\varphi).\) Ezekből végezetül a keresett metszéspontra

\(\displaystyle P=\frac{\cos(\varphi/2)}{\cos \omega}u(\varphi/2).\)

A \(\displaystyle \varepsilon\) irányvektorú, \(\displaystyle z_0\)-ra illeszkedő egyenes általános egyenlete \(\displaystyle \varepsilon \overline z - \overline \varepsilon z=\varepsilon \overline z_0 - \overline \varepsilon z_0\). Ennek segítségével felírhatjuk a vizsgált \(\displaystyle A'P\) egyenes egyenletét, ahol az irányvektor \(\displaystyle \varepsilon=A'-P=u(\varphi)-\cos(\varphi/2)u(\varphi/2)/\cos \omega\), az illeszkedő \(\displaystyle z_0\) pont pedig \(\displaystyle A'=u(\varphi)\). Először egyszerűsítsük az egyenlet jobb oldalát:

Az egyenletbe történő behelyettesítéssel megmutatjuk, hogy az \(\displaystyle A'P\) egyenesre illeszkedik az \(\displaystyle M=1/(2\cos \omega-1)\) komplex szám. Ehhez kiszámítjuk az egyenes egyenletének bal oldalát a \(\displaystyle z=M\) helyen. Kihasználjuk, hogy \(\displaystyle M\) valós, azaz megegyezik saját konjugáltjával:

Az \(\displaystyle M\) pont nem függ a \(\displaystyle \varphi\) szögtől, így az \(\displaystyle A'P\) egyenesek valóban minden állásukban egy rögzített ponton mennek át.

Diszkusszió. A feladat szövege szerint \(\displaystyle ABC\) hegyesszögű, azaz \(\displaystyle \pi/2<\omega<\pi\), így \(\displaystyle \cos \omega<0\). Speciálisan \(\displaystyle \cos \omega \neq 0\) és \(\displaystyle 2\cos \omega-1\neq 0\), így a megoldásban szereplő formulákban nem fordul elő nullával osztás, a \(\displaystyle P\) és \(\displaystyle M\) pontok léteznek, a bizonyítás minden esetben teljes.

Megjegyzés. A számolás mutatja, hogy a feladat állítása \(\displaystyle \omega \neq \pi/2\) és \(\displaystyle \omega \neq \pi/3\) esetén érvényes. Sőt, némi továbbgondolással látható, hogy a feladat állítása a két kivételes esetben is érvényes projektív értelemben: \(\displaystyle \omega=\pi/2\) esetén a \(\displaystyle P\) pont ideális, mivel \(\displaystyle BB'\parallel CC'\). Ha \(\displaystyle A'\)-n keresztül párhuzamost húzunk \(\displaystyle BB'\)-vel, akkor az illeszkedik az \(\displaystyle M=-1\) pontra. Hasonlóan, ha \(\displaystyle \omega =\pi/3\), akkor a kapott \(\displaystyle A'P\) egyenesek nem metszik egymást, hanem mindegyikük párhuzamos az \(\displaystyle ABC\) tükörtengelyével, azaz a metszéspont a tükörtengelyen lévő ideális pont.

2. megoldás (vázlat). Használjuk az előző megoldás jelöléseit, legyen az \(\displaystyle ABC\) kör középpontja \(\displaystyle O\) és számoljunk irányított szögekkel. Ekkor \(\displaystyle AOB\sphericalangle=\omega\) miatt \(\displaystyle BOC\sphericalangle=2\pi-2\omega\), és így \(\displaystyle B'OC'\sphericalangle=2\pi-2\omega\) is teljesül; vagyis a \(\displaystyle BB'\) egyenest egy \(\displaystyle O\) körüli \(\displaystyle 2\pi-2\omega\) szögű elforgatás \(\displaystyle CC'\)-be viszi, a két egyenes (\(\displaystyle P\)-nél) bezárt szöge \(\displaystyle 2\pi-2\omega\), amiből a látókörívekről szóló tétel szerint következik, hogy \(\displaystyle P\) illeszkedik az \(\displaystyle BCO\) körre.

Jelölje \(\displaystyle M\) az \(\displaystyle ABC\) és \(\displaystyle BCO\) körök belső hasonlósági pontját, és legyen \(\displaystyle \psi\) az az \(\displaystyle M\) középpontú, negatív arányú középpontos hasonlóság, amely az \(\displaystyle ABC\) kört a \(\displaystyle BCO\) körbe képezi. Megmutatjuk, hogy \(\displaystyle \psi(A')=P\), amiből az állítás következik.

Szimmetria miatt világos, hogy \(\displaystyle M\), illetve a \(\displaystyle BCO\) kör \(\displaystyle K\) középpontja is illeszkedik az \(\displaystyle AO\) egyenesre. Jelölje \(\displaystyle O'\) a \(\displaystyle BCO\) kör \(\displaystyle O\)-val átellenes pontját, ekkor \(\displaystyle \psi(A)=O'\). Elemi szögszámolással

\(\displaystyle O'KP\sphericalangle=2\cdot O'OP \sphericalangle= 2 \cdot (BOP\sphericalangle-BOO'\sphericalangle)=2 \cdot \left(\frac{\omega+\varphi}{2} -\frac{\omega}{2} \right)=\varphi.\)

Mivel a középpontos hasonlóság szögtartó, így a tény, hogy az \(\displaystyle ABC\) kör \(\displaystyle \psi\) melletti képe a \(\displaystyle BCO\) kör, \(\displaystyle \psi(A)=O'\); \(\displaystyle AOA'\sphericalangle=\varphi\) és az előbb igazolt \(\displaystyle O'KP\sphericalangle=\varphi\) együttesen implikálják, hogy \(\displaystyle \psi(A')=P\).

Statistics:

24 students sent a solution.
6 points:	Bencz Benedek, Bodor Mátyás, Chrobák Gergő, Csonka Illés, Czirják Márton Pál, Diaconescu Tashi, Fülöp Csilla, Gömze Norken, Holló Martin, Kovács Benedek Noel, Melján Dávid Gergő, Miklós Janka, Seprődi Barnabás Bendegúz, Simon László Bence, Sipos Botond Örs, Szakács Ábel, Tarján Bernát, Varga Boldizsár, Virág Lénárd Dániel, Virág Rudolf, Zömbik Barnabás.
5 points:	Tusnády Sámuel.
3 points:	2 students.

Problems in Mathematics of KöMaL, December 2022