 |
A B. 5291. feladat (2023. január) |
B. 5291. Az \(\displaystyle ABC\) háromszög beírt körének középpontja \(\displaystyle I\), körülírt körének középpontja \(\displaystyle O\). Mekkora a háromszög területe, ha \(\displaystyle OIA\sphericalangle=90^\circ\), \(\displaystyle AI=89\) és \(\displaystyle {BC=160}\)?
Javasolta: Róka Sándor (Nyíregyháza)
(5 pont)
A beküldési határidő 2023. február 10-én LEJÁRT.
Megoldás. Először egy ismert segédállítást idézünk fel a bizonyításával együtt.
Lemma. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-ból induló belső szögfelezője a körülírt kört az \(\displaystyle L\) pontban metszi. A beírt kör középpontja \(\displaystyle I\). Ekkor a \(\displaystyle B, C\) és \(\displaystyle I\) pontok egy \(\displaystyle L\) középpontú körön vannak.
Bizonyítás. Megmutatjuk, hogy a \(\displaystyle BIL\) háromszög egyenlő szárú. A \(\displaystyle BIL\sphericalangle\) az \(\displaystyle ABI\) háromszög külső szöge, így a szokásos jelölésekkel \(\displaystyle BIL\sphericalangle=ABI\sphericalangle+BAI\sphericalangle=\frac{\alpha}{2}+\frac{\beta}{2}\). Az \(\displaystyle ACB\sphericalangle=ALB\sphericalangle=ILB\sphericalangle=\gamma\), mert az \(\displaystyle AB\) húrhoz tartozó kerületi szögek.
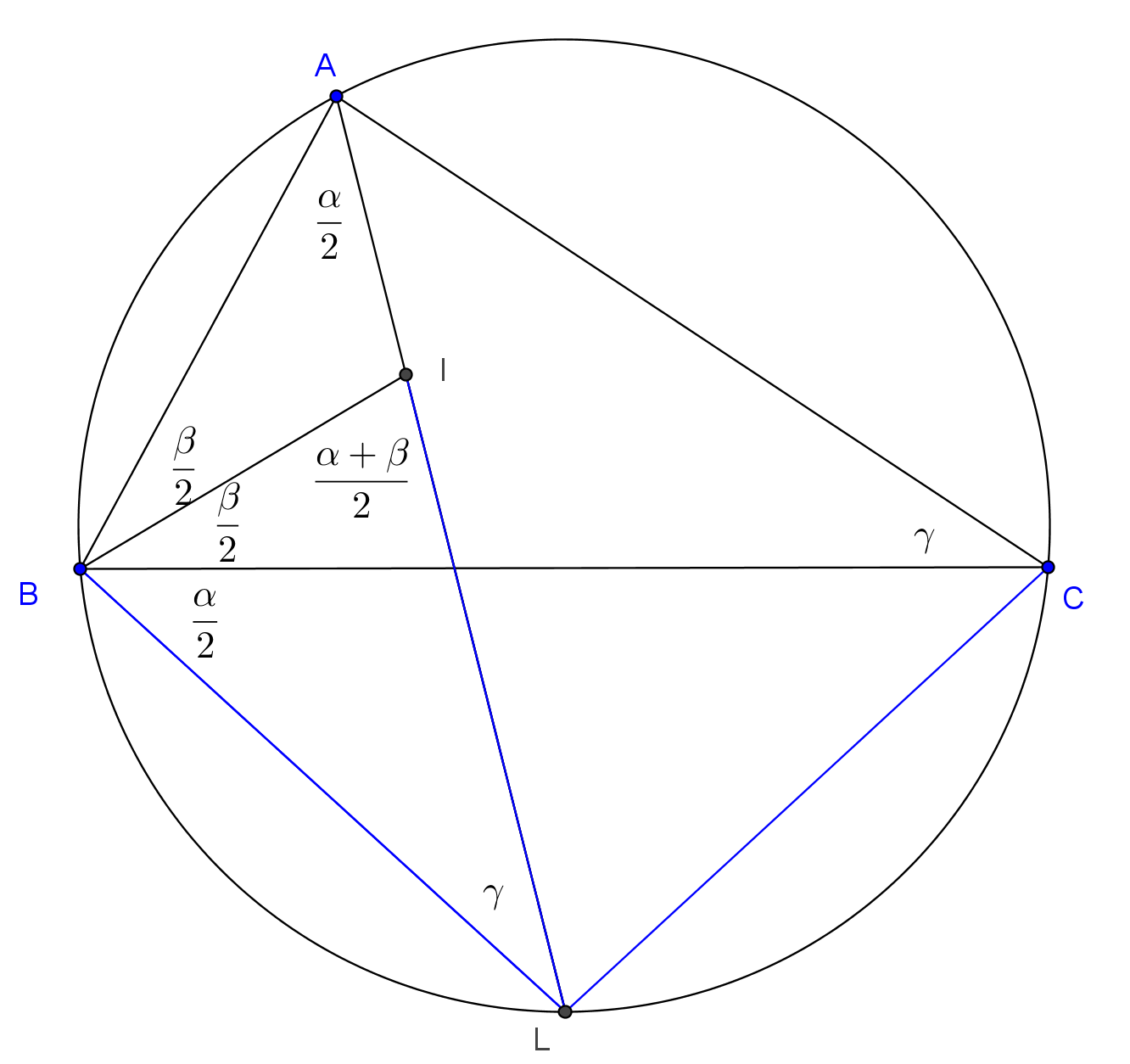
Ezek után a szögösszeg alapján \(\displaystyle IBL\sphericalangle=\frac{\alpha}{2}+\frac{\beta}{2}\), tehát a \(\displaystyle BIL\) háromszög valóban egyenlő szárú, \(\displaystyle BL=IL\). Ugyanígy igazolható az is, hogy \(\displaystyle CL=IL\).
Megjegyzés. A \(\displaystyle BC\) oldalhoz írt kör \(\displaystyle I_a\) középpontja szintén ugyanakkora távolságra van az \(\displaystyle L\) ponttól, mint a \(\displaystyle B\) és \(\displaystyle C\) csúcsok, az \(\displaystyle I, B, I_a\) és \(\displaystyle C\) pontok egy körön vannak. Ugyanez a kör már az októberi B. 5268. feladat megoldásában is fontos szerepet játszott: https://www.komal.hu/feladat?a=feladat&f=B5268&l=hu.
Most rátérhetünk a feladat megoldására. Az \(\displaystyle AL\) szakasz az \(\displaystyle ABC\) körülírt körének húrja. Felezőmerőlegese – a feltétel alapján \(\displaystyle IO\) – átmegy a kör \(\displaystyle O\) középpontján. Ezzel látjuk, hogy \(\displaystyle AI=IL=BL=89\).
A \(\displaystyle BCL\) egyenlő szárú háromszög oldalainak ismeretében meghatározzuk a körülírt kör sugarát.
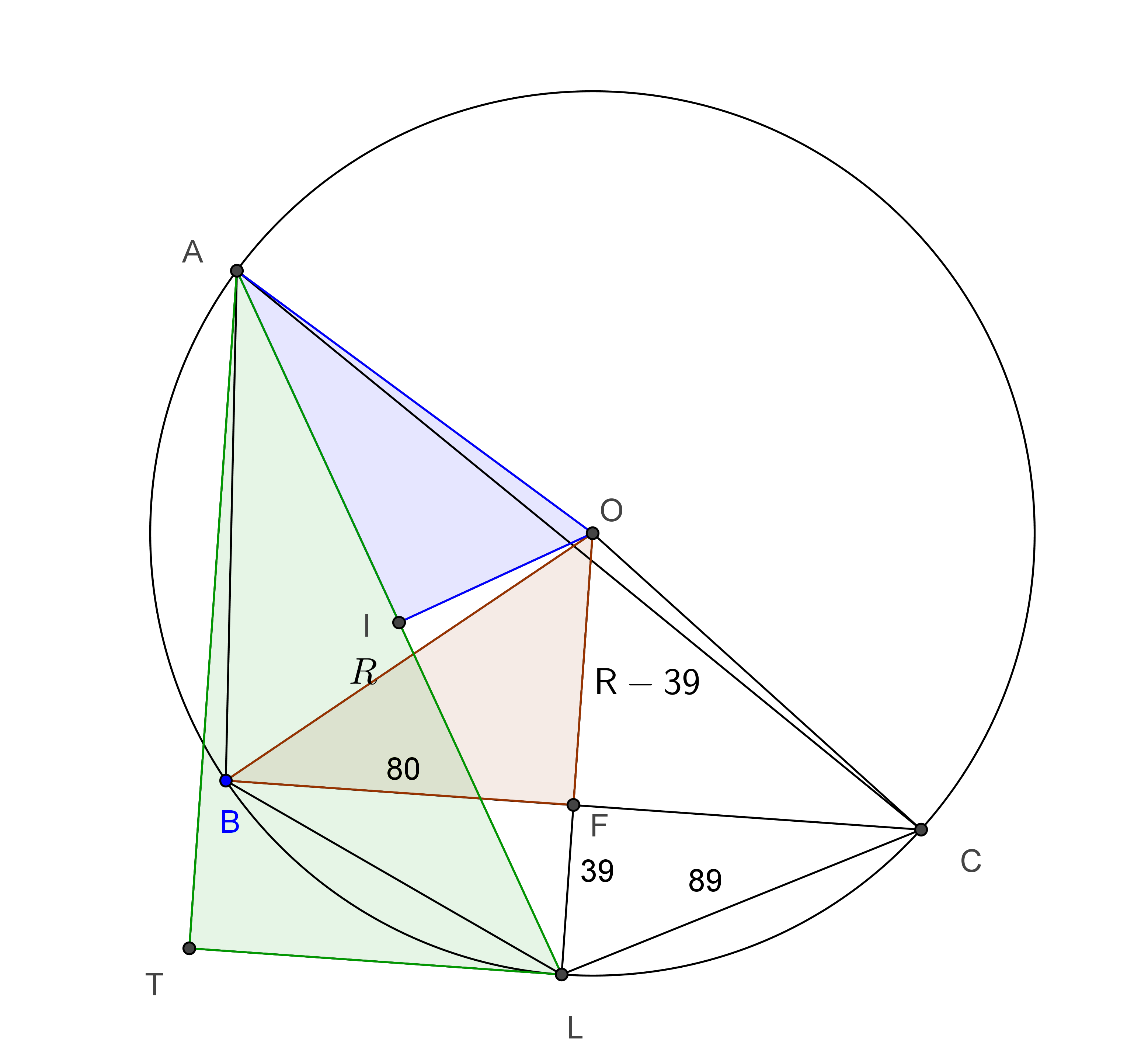
A \(\displaystyle BC\) oldal felezőpontja legyen \(\displaystyle F\). Ekkor a \(\displaystyle BFL\) derékszögű háromszögből \(\displaystyle LF^2=89^2-80^2=1521=39^2\), vagyis \(\displaystyle LF=39\). Most pedig a \(\displaystyle BFO\) háromszögre alkalmazzuk a Pitagorasz-tételt:
\(\displaystyle BO^2=BF^2+FO^2,\)
\(\displaystyle R^2=80^2+(R-39)^2,\)
\(\displaystyle R=\frac{89^2}{78}.\)
Ismert, hogy a belső szögfelező egyforma szöget zár be az ugyanahhoz a csúcshoz tartozó magasságvonallal és körülírt kör sugárral. Ezt felhasználva két hasonló háromszöget találunk az ábrán, amelyből majd az \(\displaystyle A\) csúcshoz tartozó magasság számolható.
Az \(\displaystyle A\) csúcshoz tartozó magasság egyenesére állítsunk merőlegest az \(\displaystyle L\) pontból, a talppont legyen \(\displaystyle T\). Az előbbi szögre vonatkozó megjegyzés alapján így \(\displaystyle AIO\triangle \sim ATL\triangle\). A megfelelő oldalak arányából
\(\displaystyle \frac{AT}{AL}=\frac{AI}{AO},\)
az adatokkal pedig
\(\displaystyle AT=\frac{AL\cdot AI}{AO}=\frac{2\cdot 89^2}{\frac{89^2}{78}}=156. \)
A \(\displaystyle BC\) oldalhoz tartozó magasság ebből: \(\displaystyle m_a=AT-FL=117\), és végül a háromszög területe \(\displaystyle T=80\cdot 117=9360\) területegység.
Második megoldás. Ha egy háromszögben \(\displaystyle OIA\sphericalangle=90^\circ\), akkor teljesül a \(\displaystyle b+c=2a\) összefüggés.
Ez röviden igazolható pl. a Ptolemaiosz-tétellel. A megoldás során láttuk, hogy \(\displaystyle OI\) felezőmerőlegese az \(\displaystyle AL\) szakasznak, így \(\displaystyle BL=LC=d\) és \(\displaystyle AL=2d\). Alkalmazzuk az \(\displaystyle ABLC\) húrnégyszögre Ptolemaiosz tételét:
\(\displaystyle BL\cdot AC+LC\cdot AB=BC\cdot AL,\)
\(\displaystyle d\cdot b+d\cdot c=2d\cdot a,\)
Egyszerűsítve \(\displaystyle d\)-vel:
\(\displaystyle b+c=2a.\)
Innen a beírt kör sugarát is ki tudjuk kiszámítani, hiszen ha az \(\displaystyle AB\) oldalt \(\displaystyle E\) pontban érinti a beírt kör, akkor ismert, hogy \(\displaystyle AE = s-a\), esetünkben tehát \(\displaystyle AE = \frac{b+c-a}{2} = \frac{a}2 = 80\). Az \(\displaystyle AEI\) derékszögű háromszögben:
\(\displaystyle r = \sqrt{AI^2 - AE^2} = \sqrt{89^2-80^2} = 39. \)
(Általában igaz az \(\displaystyle OIA\sphericalangle=90^\circ\) feltétel mellett, hogy \(\displaystyle r = FL\), ebből az is következik, hogy az \(\displaystyle IL\) szakaszt felezi a \(\displaystyle BC\) oldalegyenes.) Így a háromszög területe:
\(\displaystyle T = sr = \frac32 a r = 240 \cdot 39 = 9360~\text{ területegység.} \)
Statisztika:
44 dolgozat érkezett. 5 pontot kapott: Ali Richárd, Bodor Mátyás, Chrobák Gergő, Czanik Pál, Czirják Márton Pál, Diaconescu Tashi, Fehérvári Donát, Fülöp Csilla, Gömze Norken, Holló Martin, Inokai Ádám, Keresztély Zsófia, Kocsis 827 Péter, Kosztolányi Karina, Kovács Benedek Noel, Melján Dávid Gergő, Mizik Lóránt, Nguyen Kim Dorka, Sütő Áron, Szakács Ábel, Szalontai Júlia, Tarján Bernát, Teveli Jakab, Török Eszter Júlia, Varga Boldizsár, Veres Dorottya, Virág Lénárd Dániel, Virág Rudolf, Wiener Anna. 4 pontot kapott: Hetyei Dániel, Juhász-Molnár Erik, Tusnády Sámuel, Zömbik Barnabás. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2023. januári matematika feladatai
