A B. 5309. feladat (2023. március)

B. 5309. Szerkesszük meg a parabola fókuszpontját és vezéregyenesét, ha adott a tengelye és két pontja.

Javasolta: Holló Gábor (Budapest)

(6 pont)

A beküldési határidő 2023. április 11-én LEJÁRT.

Megoldás. A megoldáshoz használni fogjuk a Pascal-tételt. Ennek segítségével megszerkeszthető egy öt pontjával adott kúpszelet valamely adott pontjában az érintő:

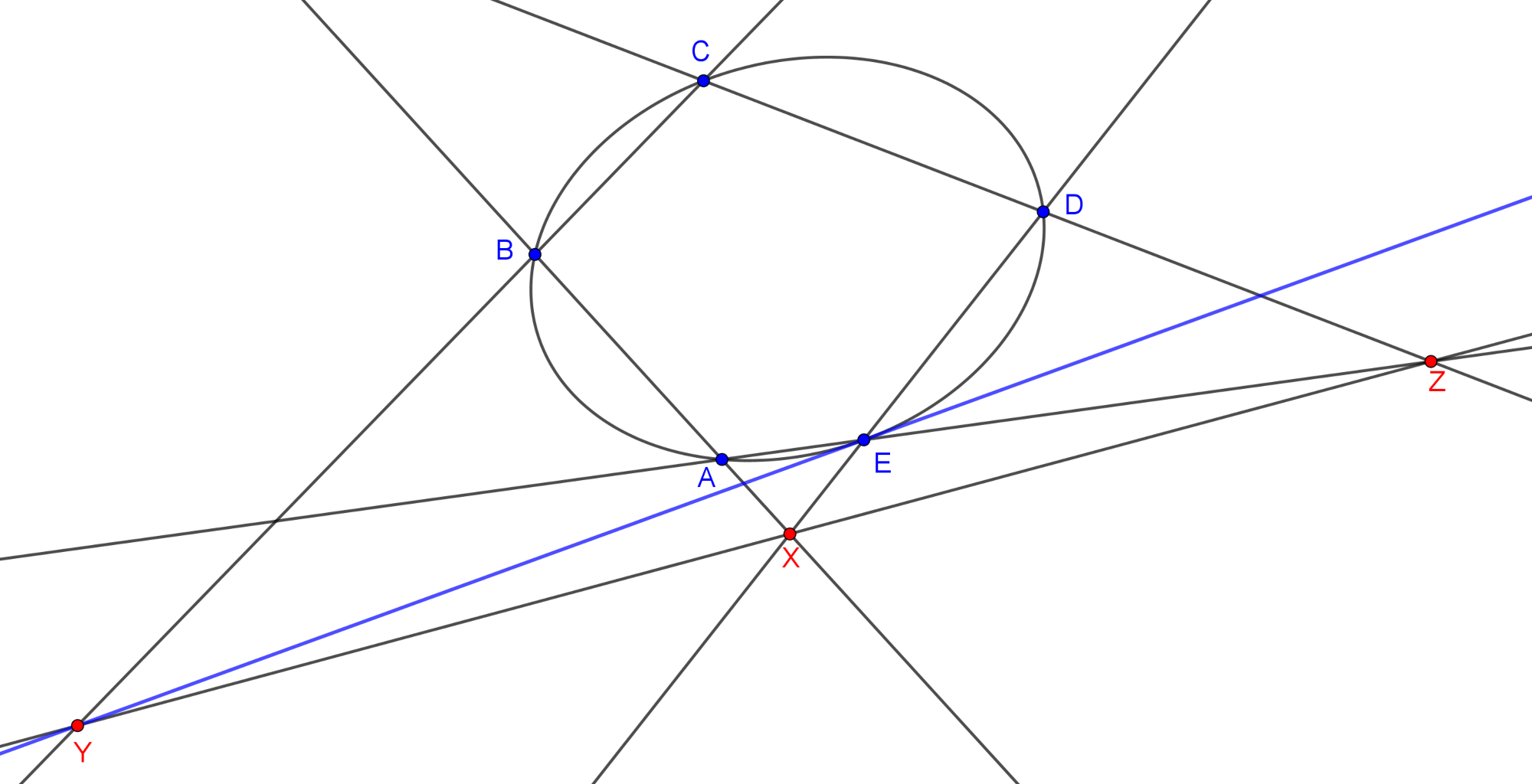
Legyen az öt adott pont \(\displaystyle A,B,C,D\) és \(\displaystyle E\), és szerkesszünk érintőt a kúpszelethez \(\displaystyle E\) pontjában. Ehhez alkalmazzuk a Pascal-tételt az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle E\) (elfajuló) ponthatosra: az \(\displaystyle X=AB\cap DE\); \(\displaystyle Y=BC\cap EE\) és \(\displaystyle Z=CD\cap EA\) pontok egy egyenesre illeszkednek (ilyenkor a tételben \(\displaystyle EE\) egyenesen az \(\displaystyle E\) pontban húzott érintőt értjük). Ez alapján a szerkesztés menete: az adott öt pontból azonnal szerkeszthető \(\displaystyle X\) és \(\displaystyle Z\), majd \(\displaystyle Y\)-t az \(\displaystyle XZ\) és \(\displaystyle BC\) egyenesek metszeteként kapjuk. A keresett érintő az \(\displaystyle EY\) egyenes.

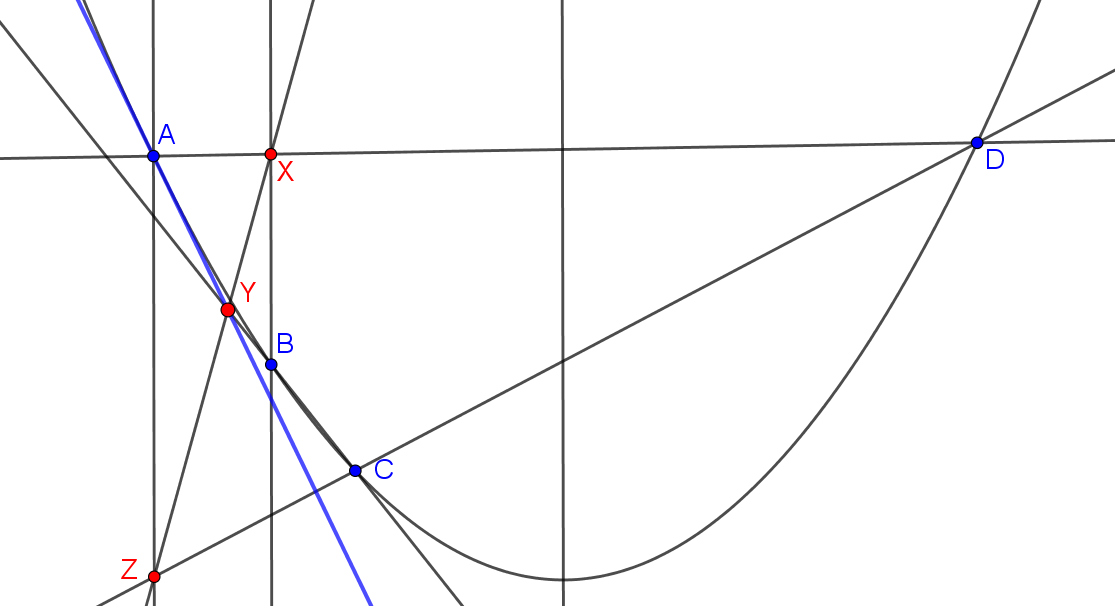
Megjegyezzük, hogy a fenti eljárás a projektív síkon további diszkusszió nélkül érvényes. Nekünk az euklídeszi síkon arra a speciális esetre lesz szükségünk, amikor egy parabolán adott négy különböző \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pont, valamint adott a parabola \(\displaystyle t\) tengelye (utóbbi lényegében a parabola ideális pontját adja meg), és az \(\displaystyle A\)-ban húzott érintőt kell megszerkesztenünk. Ekkor az eljárás a következőképpen írható le, ahol az egyszerűség kedvéért használjuk a \(\displaystyle t_P\) jelölést a \(\displaystyle P\)-re illeszkedő, \(\displaystyle t\)-vel párhuzamos egyenesre, tetszőleges \(\displaystyle P\) pont esetén: Szerkesszük meg az \(\displaystyle X=t_B\cap DA\) és \(\displaystyle Z=CD\cap t_A\) pontokat. Ezután szerkesszük meg az \(\displaystyle Y=BC\cap XZ\) pontot. Az \(\displaystyle AY\) a keresett érintő.

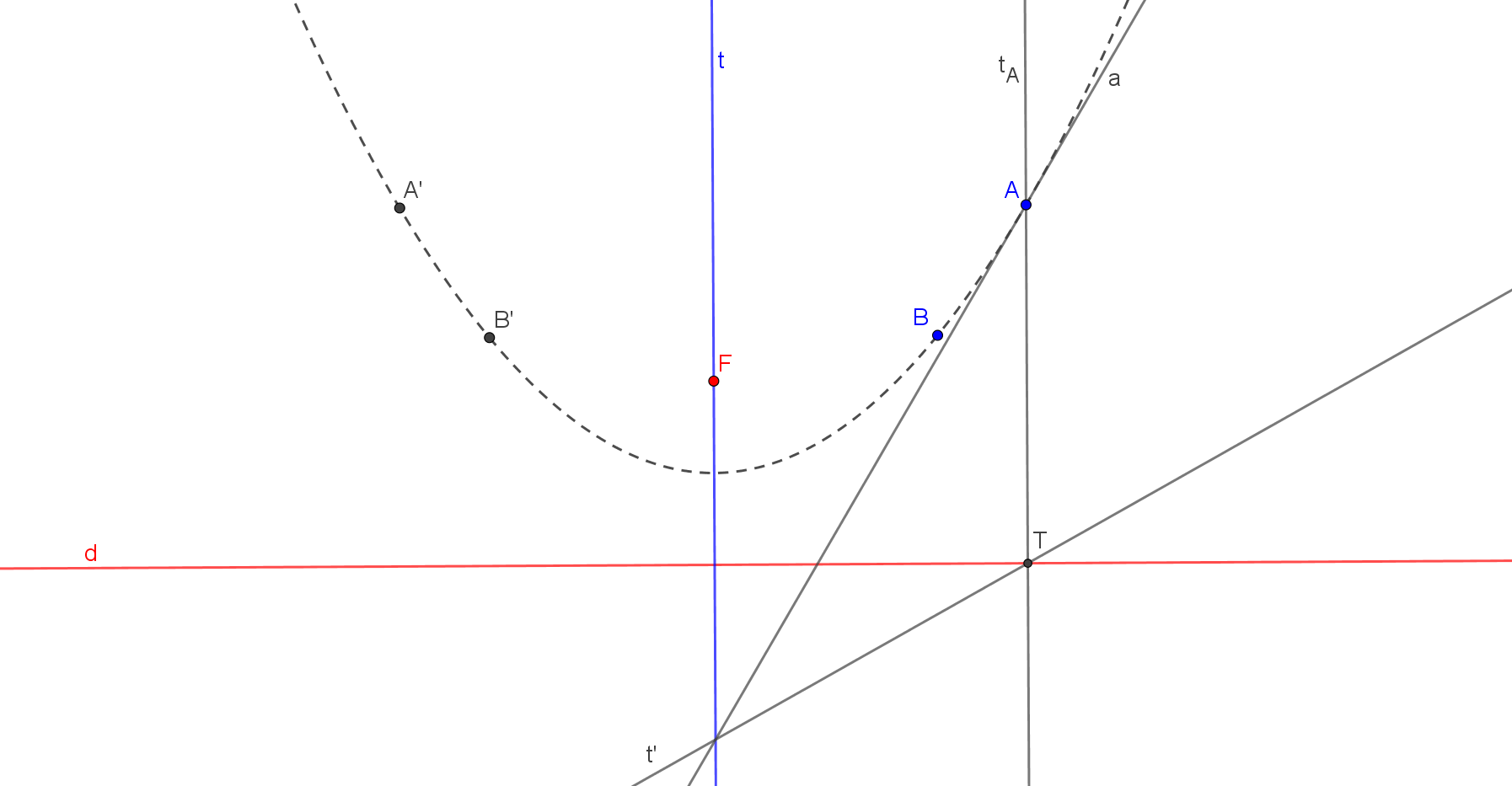
Továbbá használni fogjuk a parabola következő jól ismert tulajdonságait is (lásd például: Czapári-Soós: Geometriai feladatok gyűjteménye II., 1152. feladat): Legyen egy parabola fókusza \(\displaystyle F\), vezéregyenese \(\displaystyle d\), tengelye \(\displaystyle t\). Tekintsük a parabola egy tetszőleges \(\displaystyle E\) pontját, az \(\displaystyle E\)-ben húzott érintő legyen \(\displaystyle e\), az \(\displaystyle E\)-ből a vezéregyenesre bocsájtott merőleges talppontja \(\displaystyle T\). Ekkor \(\displaystyle F\) \(\displaystyle e\)-re vonatkozó tükörképe éppen \(\displaystyle T\). Következésképpen ha tükrözzük \(\displaystyle t\)-t \(\displaystyle e\)-re, akkor az így kapott \(\displaystyle t'\) egyenes, \(\displaystyle d\) és \(\displaystyle ET\) egy közös pontban, \(\displaystyle T\)-ben metszik egymást.

Ezek alapján a következő szerkesztési eljárást adhatjuk.

1. Legyen adott a \(\displaystyle t\) egyenes, valamint az \(\displaystyle A\) és \(\displaystyle B\) pontok.
2. Szerkesszük meg \(\displaystyle A\) és \(\displaystyle B\) \(\displaystyle t\)-re vonatkozó \(\displaystyle A'\) és \(\displaystyle B'\) tükörképeit.
3. A fenti módszerrel szerkesszük meg az \(\displaystyle A\), \(\displaystyle A'\), \(\displaystyle B\) és \(\displaystyle B'\) pontok, valamint a \(\displaystyle t\) tengely segítségével a parabolához \(\displaystyle A\)-ban húzott \(\displaystyle a\) érintőjét.
4. Szerkesszünk \(\displaystyle A\)-n keresztül \(\displaystyle t_A\) párhuzamost \(\displaystyle t\)-vel.
5. Messe a \(\displaystyle t\) tengely \(\displaystyle a\)-ra vonatkozó \(\displaystyle t'\) tükörképe \(\displaystyle t_A\)-t \(\displaystyle T\)-ben.
6. \(\displaystyle T\) pont tükörképe \(\displaystyle a\)-ra adja a keresett fókuszpontot, míg a \(\displaystyle T\)-ből \(\displaystyle t\)-re bocsájtott merőleges a keresett vezéregyenes.

Előrebocsájtott megjegyzéseink igazolják a szerkesztés helyességét.

Diszkusszió. Nyilvánvalóan nincs megoldása a feladatnak, ha az adott \(\displaystyle A\) és \(\displaystyle B\) pontokat összekötő egyenes párhuzamos a \(\displaystyle t\) tengellyel, vagy ha \(\displaystyle AB\) merőleges a \(\displaystyle t\) tengelyre, de \(\displaystyle A\) és \(\displaystyle B\) nem egymás tükörképei.

Ha \(\displaystyle A\) és \(\displaystyle B\) tükrösek \(\displaystyle t\)-re, akkor egy további, \(\displaystyle AB\)-re nem illeszkedő \(\displaystyle C\) pontot tetszőlegesen felvéve a parabola a mutatott módon megszerkeszthető, azaz ilyenkor végtelen sok megoldás van.

Ha a pontok közül pontosan az egyik, mondjuk \(\displaystyle A\), illeszkedik a tengelyre (és \(\displaystyle AB\) nem merőleges \(\displaystyle t\)-re), akkor a megadott szerkesztési eljárás nem működik. Ilyenkor az \(\displaystyle A\)-ban húzott \(\displaystyle a\) csúcsérintő egyszerűen a \(\displaystyle t\)-re \(\displaystyle A\)-ban állított merőleges. A \(\displaystyle B\) pont \(\displaystyle a\)-ra vett merőleges vetülete legyen \(\displaystyle T_a\); az \(\displaystyle AT_a\) szakasz felezőpontja \(\displaystyle M\). Ekkor szintén a korábban idézett feladat szerint \(\displaystyle BM\) a \(\displaystyle B\)-ben húzott érintő, s innen a szerkesztés a korábban látott módon befejezhető. Pontosan egy megoldás van.

Minden más esetben pontosan egy megoldás van, amit a megadott eljárás szolgáltat.

Statisztika:

46 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Bencz Benedek, Bodor Mátyás, Chrobák Gergő, Czanik Pál, Czirják Márton Pál, Diaconescu Tashi, Fajszi Karsa, Gömze Norken, Guthy Gábor, Holló Martin, Jármai Roland, Juhász-Molnár Erik, Kocsis 827 Péter, Kovács Benedek Noel, Nguyen Kim Dorka, Petrányi Lilla, Prohászka Bulcsú, Sági Mihály, Szakács Ábel, Szemlér Bálint, Tarján Bernát, Varga Boldizsár, Veres Dorottya, Zhai Yu Fan.
5 pontot kapott:	Christ Miranda Anna, Csonka Illés, Nagy 429 Leila, Op Den Kelder Ábel, Tran Dávid, Virág Lénárd Dániel, Virág Rudolf, Zömbik Barnabás.
4 pontot kapott:	4 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2023. márciusi matematika feladatai