 |
A B. 5327. feladat (2023. szeptember) |
B. 5327. Az \(\displaystyle ABC\) háromszög magasságai \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\). Tegyük fel, hogy az \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\) oldalakkal szerkeszthető háromszög, és ennek a háromszögnek a magasságai \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\). Mutassuk meg, hogy az \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) oldalakkal is szerkeszthető háromszög.
Javasolta: Vigh Viktor, Sándorfalva
(4 pont)
A beküldési határidő 2023. október 10-én LEJÁRT.
Megoldás. Az \(\displaystyle ABC\) háromszög oldalait a szokásos módon \(\displaystyle a\)-val, \(\displaystyle b\)-vel és \(\displaystyle c\)-vel jelölve felírhatjuk háromféleképpen a kétszeres területét: \(\displaystyle 2T=am_a=bm_b=cm_c\).
Ugyanezt a gondolatot megismételhetjük az \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\) oldalakkal szerkesztett háromszögre is, amelynek területét jelöljük \(\displaystyle T_1\)-gyel: \(\displaystyle 2T_1=m_ax=m_by=m_cz\).
A két egyenlőségláncolat megfelelő elemeit elosztva egymással azt kapjuk, hogy
\(\displaystyle \frac {T_1}{T}=\frac xa =\frac yb= \frac zc.\)
Ebből következik, hogy ha az \(\displaystyle ABC\) háromszögre egy \(\displaystyle \lambda=T_1/T\) arányú hasonlósági transzformációt alkalmazunk, akkor egy olyan háromszöget kapunk, aminek oldalai éppen \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\), ami miatt \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) oldalakkal valóban szerkeszthető háromszög.
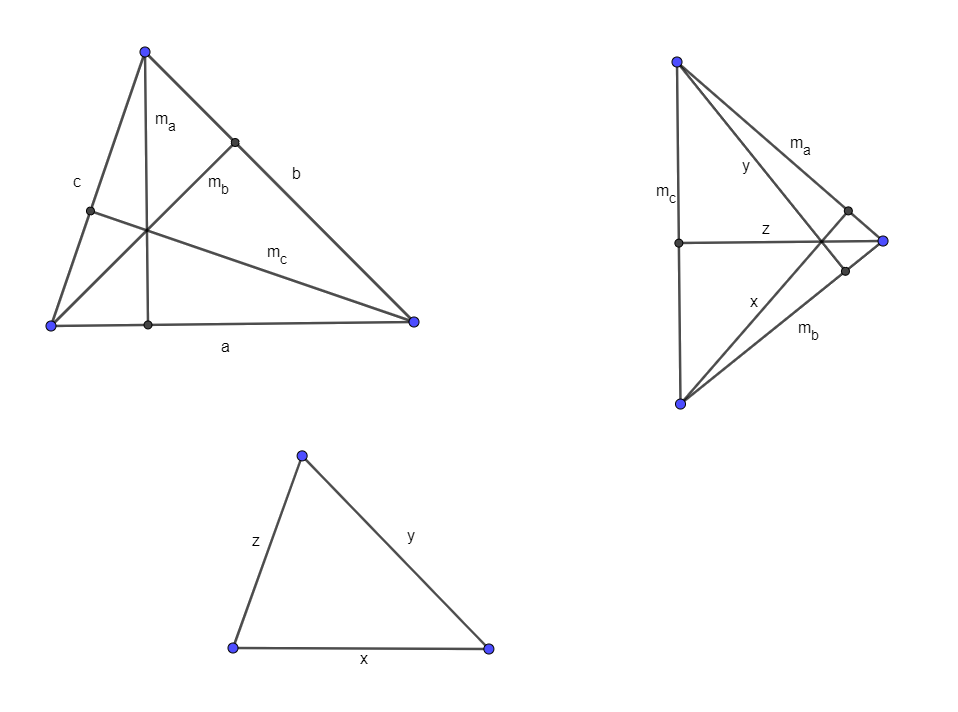
Megjegyzés. Folklór feladat, hogy szerkesszünk háromszöget, ha adott a három magassága. Az elterjedt módszer felhasználja a feladat megoldásában is kimutatott tényt: az \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\) oldalakkal szerkesztett háromszög magasságaiból szerkesztett háromszög hasonló a keresetthez. A szerkesztés (vázlatos) menete:
- Szerkesszünk \(\displaystyle \Delta_1\) háromszöget \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\) oldalakkal.
- Szerkesszük meg \(\displaystyle \Delta_1\) háromszög \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) magasságait.
- Szerkesszünk \(\displaystyle \Delta_2\) háromszöget \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) oldalakkal. Jelölje \(\displaystyle \Delta_2\)-ben az \(\displaystyle x\)-hez tartozó magasságot \(\displaystyle m\).
- Nagyítsuk ki \(\displaystyle \Delta_2\) háromszöget \(\displaystyle m_a/m\) arányban.
Vegyük észre, hogy ez az eljárás a folklór szerkesztési feladatra hiányos! Ugyanis az \(\displaystyle m_a\), \(\displaystyle m_b\) és \(\displaystyle m_c\) oldalakkal nem biztos, hogy szerkeszthető háromszög; annak ellenére, hogy a feladatnak van megoldása. (Vegyük például az egyenlő szárú háromszöget, aminek oldalai \(\displaystyle 1000\), \(\displaystyle 1000\) és \(\displaystyle 1\). Ennek magasságai körülbelül \(\displaystyle 1\), \(\displaystyle 1\) és \(\displaystyle 1000\) hosszúak, nyilvánvalóan nem teljesítik a háromszög-egyenlőtlenséget.)
Egy lehetséges helyes, és mindig működő módszer, ha \(\displaystyle 1/m_a\), \(\displaystyle 1/m_b\) és \(\displaystyle 1/m_c\) oldalakkal szerkesztünk háromszöget, és azt nagyítjuk ki megfelelő arányban.
Statisztika:
119 dolgozat érkezett. 4 pontot kapott: 85 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 7 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2023. szeptemberi matematika feladatai

