 |
A B. 5337. feladat (2023. október) |
B. 5337. Egy szabályos \(\displaystyle n\)-szög minden oldalára megrajzoltam kifelé egy szabályos háromszöget. A háromszögek harmadik csúcsai egy nagyobb szabályos \(\displaystyle n\)-szöget alkotnak. Mennyi lehet \(\displaystyle n\), ha a két sokszög területének aránya egész szám?
Javasolta: Hujter Bálint (Budapest)
(4 pont)
A beküldési határidő 2023. november 10-én LEJÁRT.
Megoldás. Jelölje \(\displaystyle A_1 A_2 A_3 \ldots A_{n-1} A_n\) az eredeti (kisebb) szabályos \(\displaystyle n\)-szöget, és jelölje \(\displaystyle B_i\) az \(\displaystyle A_iA_{i+1}\) oldalra rajzolt szabályos háromszög harmadik csúcsát, így a nagyobb szabályos \(\displaystyle n\)-szög \(\displaystyle B_1 B_2 B_3 \ldots b_{n-1} B_n\).
Jelölje a kisebbik szabályos \(\displaystyle n\)-szög oldalhosszát \(\displaystyle a\), a nagyobbikét \(\displaystyle b\). Mivel a két szabályos \(\displaystyle n\)-szög hasonló, ezért területük aránya \(\displaystyle \dfrac{b^2}{a^2}\).
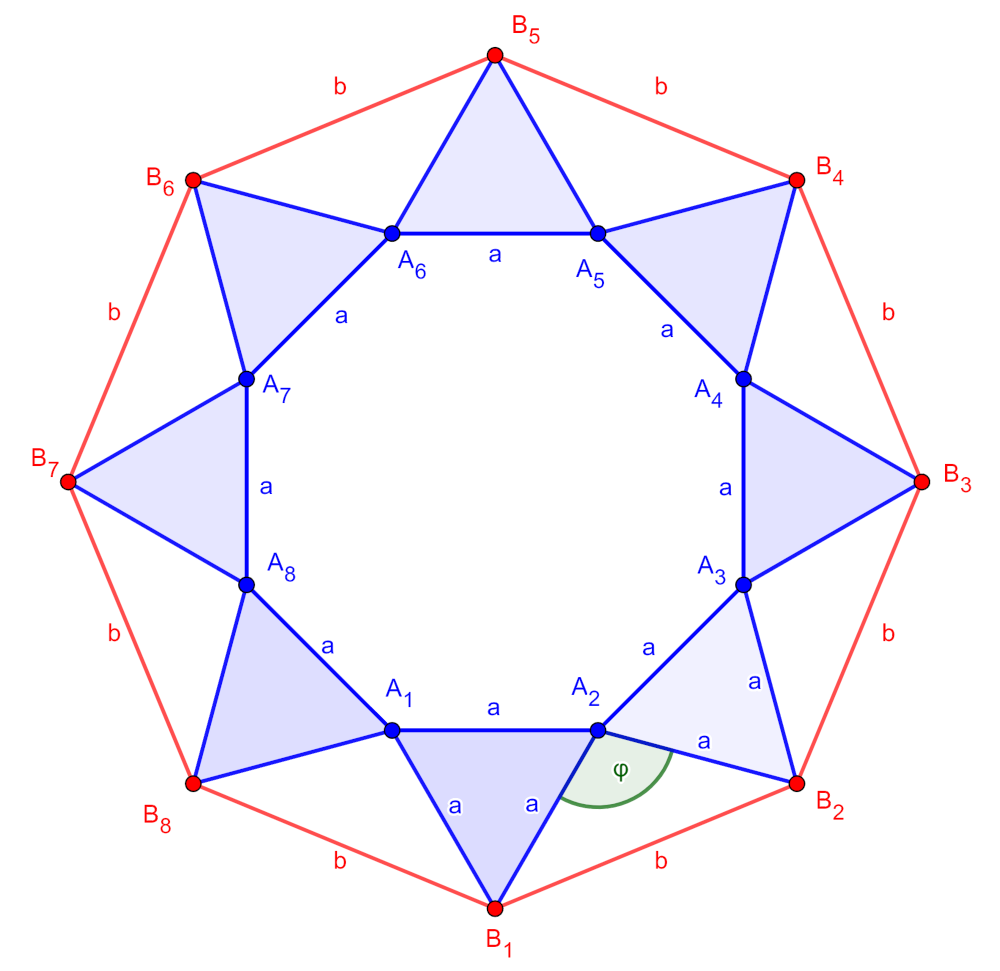
Tekintsük az \(\displaystyle A_1A_2B_1\) egyenlő szárú háromszöget. Jelölje \(\displaystyle \varphi\) a két \(\displaystyle a\) hosszúságú oldala által bezárt szöget. Mivel a szabályos \(\displaystyle n\)-szög egy belső szöge \(\displaystyle \frac{n-2}{n} \cdot 180^{\circ}\), ezért \(\displaystyle \varphi = 360^{\circ} - \frac{n-2}{n} \cdot 180^{\circ} - 2 \cdot 60^{\circ} = 60^{\circ} + \frac{360^\circ}{n}\).
Ha \(\displaystyle n=3\), akkor \(\displaystyle \varphi = 180^{\circ}\), ilyenkor az \(\displaystyle A_1A_2B_1\) háromszög egy szakasszá fajul.
\(\displaystyle n > 3\) esetén \(\displaystyle 60^{\circ} < \varphi < 180^{\circ}\), így az \(\displaystyle A_1A_2B_1\) háromszög tényleg létezik (méghozzá az ábrán látható elrendezésben: a nagyobb szabályos \(\displaystyle n\)-szög tartalmazza, míg a kisebbik szabályos \(\displaystyle n\)-szög nem tartalmazza az \(\displaystyle A_1A_2B_1\) háromszöget).
Felírhatjuk a koszinusztételt (az egyenlet \(\displaystyle \varphi = 180^{\circ}\) esetben is teljesül):
\(\displaystyle b^2 = a^2 + a^2 - 2a^2 \cos \varphi, \)
azaz
\(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi. \)
Így a két terület aránya pontosan akkor lesz egész, ha \(\displaystyle \cos \varphi\) egy egész szám fele. Mivel \(\displaystyle 60^{\circ} < \varphi \le 180^{\circ}\), ezért \(\displaystyle \cos \varphi\) a \(\displaystyle \left[-1,\frac12 \right)\) intervallumból vehet fel értékeket, így a következő értékek jöhetnek szóba:
\(\displaystyle \cos \varphi_1 = -1, \quad \cos \varphi_2 = -\frac12 \quad \text{és} \quad \cos \varphi_3 = 0 \quad \)
Már korábban láttuk, hogy az \(\displaystyle n_1 = 3\) esetben lesz \(\displaystyle \cos \varphi_1 = \cos 180^{\circ} = -1\), ilyenkor a két szabályos 3-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_1 = 4\).
Ha \(\displaystyle \cos \varphi_2 = -\frac12\), akkor \(\displaystyle \varphi_2 = 120^{\circ} = 60^{\circ} + \frac{360^\circ}{n_2}\), azaz \(\displaystyle n_2 = 6\). A két szabályos 6-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_2 = 3\).
Ha \(\displaystyle \cos \varphi_3 = 0\), akkor \(\displaystyle \varphi_3 = 90^{\circ} = 60^{\circ} + \frac{360^\circ}{n_1}\), azaz \(\displaystyle n_1 = 12\). A két szabályos 12-szög területének aránya \(\displaystyle \frac{b^2}{a^2} = 2 - 2 \cos \varphi_3 = 2\).
Összefoglalva: \(\displaystyle n \in \{ 3,6,12 \}\) esetén lesz a két sokszög területének aránya egész szám.
Statisztika:
121 dolgozat érkezett. 4 pontot kapott: 76 versenyző. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 4 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 5 dolgozat.
A KöMaL 2023. októberi matematika feladatai

