 |
A B. 5352. feladat (2023. december) |
B. 5352. Milyen \(\displaystyle n > 3\) egész számok esetén lehet úgy megadni \(\displaystyle n\) egyenest a síkon, hogy közülük bármely három egyenlő szárú háromszöget alkosson?
Javasolta: Hujter Bálint (Budapest)
(4 pont)
A beküldési határidő 2024. január 10-én LEJÁRT.
1. megoldás. Könnyen ellenőrizhető, hogy egy szabályos ötszög oldalegyenesei közül bármely három egyenlő szárú háromszöget határol, így \(\displaystyle n\le 5\) esetén léteznek megfelelő egyenesek.
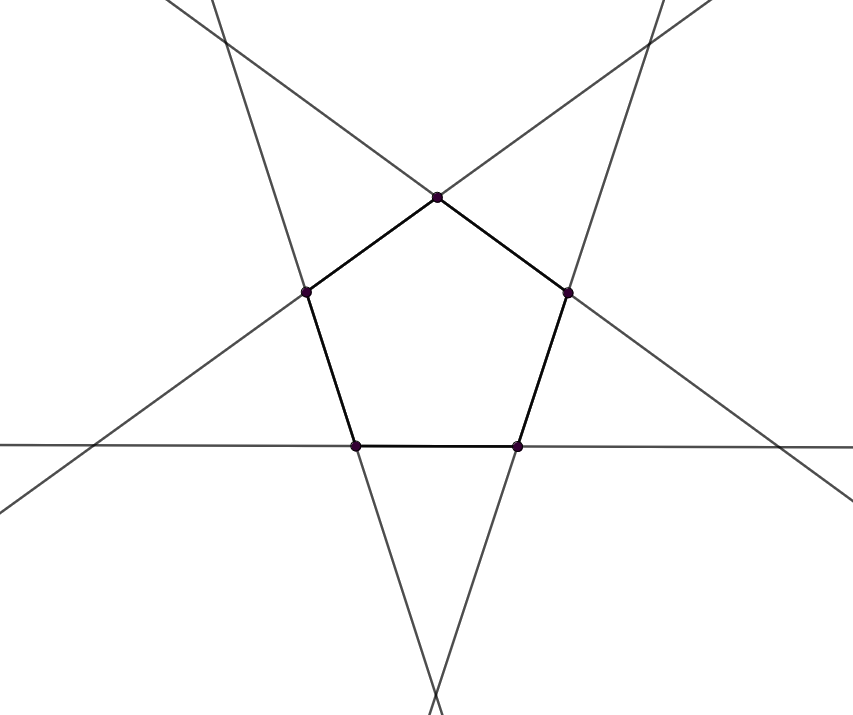
Megmutatjuk, hogy hat, a feltételeknek megfelelő egyenes már nem létezik. Világos, hogy az egyenesek szükségképpen általános helyzetűek (nincsen közöttük sem három egy pontra illeszkedő, sem párhuzamosak), továbbá ha egy jó konfigurációban egy egyenest eltolunk, attól a konfiguráció helyessége nem változik, vagyis elegendő az egyenesek irányát figyelni.
Rögzítsünk egy \(\displaystyle e\), \(\displaystyle f\) metsző egyenespárt, amelyek nem derékszöget zárnak be (ilyen létezése feltehető). Ekkor tetszőleges \(\displaystyle g\) egyenesre ha az \(\displaystyle e\), \(\displaystyle f\), \(\displaystyle g\) hármas által alkotott egyenlő szárú háromszög alapja \(\displaystyle e\) vagy \(\displaystyle f\), akkor \(\displaystyle g\) iránya egyértelműen meghatározott. Ha \(\displaystyle g\) az alap, akkor merőleges \(\displaystyle e\) és \(\displaystyle f\) valamelyik szögfelezőjére, tehát itt további két, egymásra merőleges irány jöhet szóba. Összesen – \(\displaystyle e\) és \(\displaystyle f\) irányát is számítva – máris csak hat lehetséges irányunk van, amiből kettő, mondjuk \(\displaystyle g_1\) és \(\displaystyle g_2\) merőleges. Viszont vegyük észre, hogy \(\displaystyle g_1\)-t és \(\displaystyle g_2\)-t rögzítve a harmadik egyenes csak két irányban vehető hozzájuk, mivel egyenlő szárú háromszög alapon fekvő szöge nem lehet derékszög, tehát a kapott hat irány sem lehet megfelelő.
2. megoldás. Tegyük fel, hogy \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\), \(\displaystyle e\) és \(\displaystyle f\) hat, a kívánalmaknak megfelelő egyenes. Közülük tetszőleges három \(\displaystyle x,y\) és \(\displaystyle z\) egyenes egyenlő szárú háromszöget alkot, jelölje \(\displaystyle (x;y,z)\) azt az állítást, hogy ennek a háromszögnek \(\displaystyle x\) az alapegyenese; \(\displaystyle y\) és \(\displaystyle z\) pedig a száregyenesei. Ha a meghatározott háromszög szabályos, tetszőleges oldalegyenes választható alapnak, de minden egyeneshármasra kiválasztunk és lerögzítünk alapot.
Az általánosság megszorítása nélkül feltehető, hogy \(\displaystyle (a;b,c)\). Ekkor ha \(\displaystyle x\in \{d,e,f\}\), akkor \(\displaystyle (a;b,x)\) és \(\displaystyle (a;c,x)\) egyike sem állhat fenn, ugyanis előbbi esetben \(\displaystyle x\parallel c\), utóbbi esetben \(\displaystyle x\parallel b\) következne, ami a feltétel szerint nem lehet. Hasonló megfontolással látható, hogy \(\displaystyle (a;d,e)\), \(\displaystyle (a;d,f)\) és \(\displaystyle (a;e,f)\) közül legfeljebb egy teljesülhet. Összegezve azt kaptuk, hogy \(\displaystyle a\) legfeljebb két háromszögben lehet alap.
Az előző gondolatmenetet \(\displaystyle a\) helyett tetszőleges egyenesre elmondhatjuk, következésképp bármely egyenes legfeljebb kettő háromszögben lehet alap, így legfeljebb \(\displaystyle 6\cdot 2=12\) háromszögünk lehet. Mivel hat egyenesből három húszféleképpen választható ki, így ellenmondásra jutottunk, nem létezik hat, a feltételeknek megfelelő egyenes.
Tehát pontosan akkor létezik \(\displaystyle n\) darab a feltételeknek megfelelő egyenes, ha \(\displaystyle n\le 5\).
Megjegyzés. Világos, hogy egy konfiguráció helyessége nem változik, ha a benne szereplő egyeneseket eltoljuk (ügyelve az általános helyzet megtartására). A megoldásban használt módszerrel, és rövid szögszámolással megmutatható, hogy \(\displaystyle n=5\) esetén a szabályos ötszög lényegében az egyetlen jó konstrukció.
Statisztika:
102 dolgozat érkezett. 4 pontot kapott: 74 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 8 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2023. decemberi matematika feladatai

