 |
A B. 5367. feladat (2024. február) |
B. 5367. \(\displaystyle a)\) Az egységnyi sugarú nyílt körlapban elhelyeztünk egymásra merőlegesen két \(\displaystyle \ell\) hosszúságú nyílt szakaszt úgy, hogy a szakaszoknak nincs közös pontjuk. Mennyi lehet \(\displaystyle \ell\)?
\(\displaystyle b)\) Az egységnyi sugarú nyílt gömbben elhelyeztünk három \(\displaystyle \ell\) hosszúságú nyílt szakaszt úgy, hogy páronként merőlegesek, és semelyik kettőnek nincs közös pontja. Mennyi lehet \(\displaystyle \ell\)?
Javasolta: Vígh Viktor (Sándorfalva)
(4 pont)
A beküldési határidő 2024. március 11-én LEJÁRT.
Megoldás. Nyilvánvalóan mindkét esetben \(\displaystyle 0<\ell<2\), hiszen sem a kör, sem a gömb nem tartalmaz az átmérőjénél hosszabb szakaszt, \(\displaystyle \ell=2\) esetén pedig a szakaszok a kör, ill. a gömb középpontjában metszenék egymást.
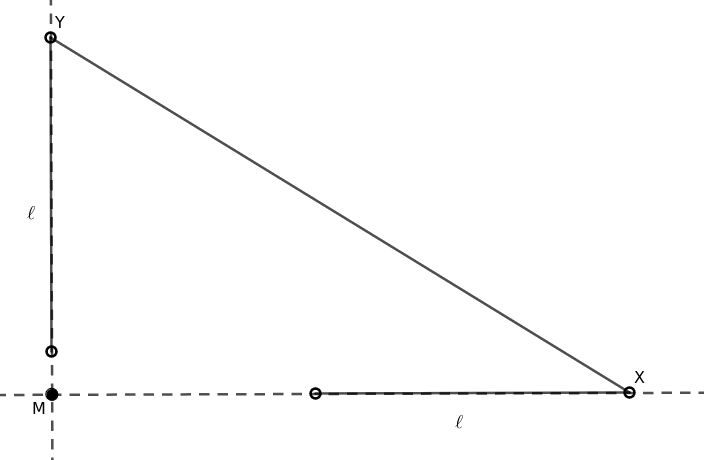
Most rátérünk az a) részre. Legyen a szakaszok tartóegyeneseinek metszéspontja \(\displaystyle M\). Először tegyük fel, hogy \(\displaystyle M\) nem illeszkedik egyik szakaszra sem. Legyenek a szakaszoknak az \(\displaystyle M\)-től távolabbi végpontjai \(\displaystyle X\), illetve \(\displaystyle Y\). Ekkor \(\displaystyle MXY\) egy derékszögű háromszög, amelynek derékszögű csúcsa \(\displaystyle M\), és amelynek mindkét befogója legalább \(\displaystyle \ell\) hosszúságú. A Pitagorasz-tételből következik, hogy \(\displaystyle XY\ge \ell \sqrt2\). Másrészt a feltételek szerint \(\displaystyle X\)-t és \(\displaystyle Y\)-t a körlap lezártja tartalmazza, ezért \(\displaystyle XY\le 2\). Ezekből \(\displaystyle \ell \le \sqrt 2\) adódik.
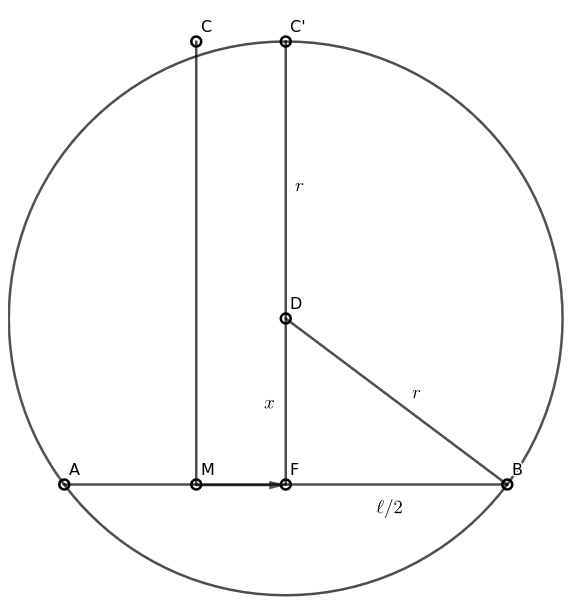
Most tegyük fel, hogy \(\displaystyle M\) az elhelyezett \(\displaystyle AB\) szakasz egy pontja, a másik szakasz \(\displaystyle M\)-től távolabbi végpontja legyen \(\displaystyle C\). Világos, hogy a második szakaszt \(\displaystyle M\) irányába eltolva a körön belül marad, ezért feltehető, hogy a második szakasz éppen \(\displaystyle MC\). A feltételek szerint az \(\displaystyle ABC\) háromszög körülírt körének sugara legfeljebb egységnyi.
Legyen \(\displaystyle AB\) felezőpontja \(\displaystyle F\), és toljuk el \(\displaystyle C\) pontot \(\displaystyle \overrightarrow{MF}\)-ral, így kapjuk \(\displaystyle C'\) pontot. Világos, hogy az \(\displaystyle ABC'\) háromszöget is tartalmazza az \(\displaystyle ABC\) háromszög körülírt köre (hiszen a \(\displaystyle C\) pont \(\displaystyle C'F\)-re vonatkozó tükörképe rajta van a körvonalon), ezért \(\displaystyle ABC'\) körülírt körének sugara is legfeljebb egységnyi. Másrészről \(\displaystyle ABC'\) körülírt körének sugara kifejezhető \(\displaystyle \ell\) segítségével; az ábra szerint \(\displaystyle (\ell/2)^2+x^2=r^2\) és \(\displaystyle x+r=\ell\). Ebből \(\displaystyle x=\ell-r\)-t visszahelyettesítve \(\displaystyle r=5\ell/8\) adódik. Innen \(\displaystyle r\le 1\) észrevételünk miatt \(\displaystyle \ell\le 8/5\).
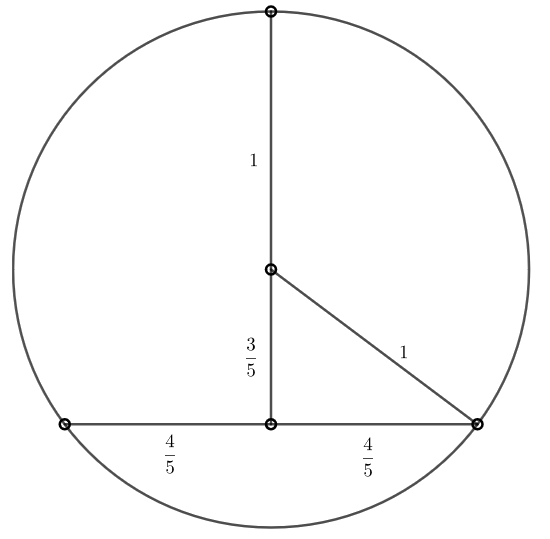
Mindkét vizsgált esetben teljesül tehát, hogy \(\displaystyle \ell\le 8/5\). Könnyen látható, hogy az ábra szerinti elrendezésben \(\displaystyle \ell=8/5\) megvalósítható. Továbbá a szakaszokat a megfelelő arányban kicsinyítve a középpontjaikból minden \(\displaystyle 0<\ell<8/5\) is megvalósítható. Ezért az a) esetben \(\displaystyle 0<\ell\le 8/5\).
Rátérünk a b) részre; megmutatjuk, hogy itt minden \(\displaystyle 0<\ell<2\) lehetséges. Rögzítsünk egy \(\displaystyle 0<\ell<2\) értéket, legyen
\(\displaystyle 0<d=\sqrt{1-(\ell/2)^2}<1, \)
és helyezzük el a gömbünket a térbeli derékszögű koordinátarendszerben úgy, hogy közzépontja az origóba essen.
Tekintsük most az \(\displaystyle xy\)-síkban az \(\displaystyle x=d\) egyenletű egyenest, az \(\displaystyle yz\)-síkban az \(\displaystyle y=d\) egyenest; és az \(\displaystyle xz\)-síkban a \(\displaystyle z=d\) egyenletű egyenest. Ezek páronként egymásra merőleges, kitérő egyenesek, amelyek a nyílt gömböt egy-egy nyílt, \(\displaystyle \ell\) hosszúságú (és szükségképpen páronként idegen) szakaszban metszik. Ez a példa mutatja, hogy valóban minden \(\displaystyle 0<\ell<2\) lehetséges.
Statisztika:
105 dolgozat érkezett. 4 pontot kapott: 56 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 25 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 10 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2024. februári matematika feladatai

