A B. 5369. feladat (2024. február)

B. 5369. Az \(\displaystyle ABC\) szabályos háromszög \(\displaystyle P\) belső pontjára \(\displaystyle APB\sphericalangle=150^\circ\). Mutassuk meg, hogy \(\displaystyle PA^2+PB^2=PC^2\).

Javasolta: Vígh Viktor (Sándorfalva)

(4 pont)

A beküldési határidő 2024. március 11-én LEJÁRT.

1. megoldás. Használjuk az alábbi ábrát és jelöléseit!

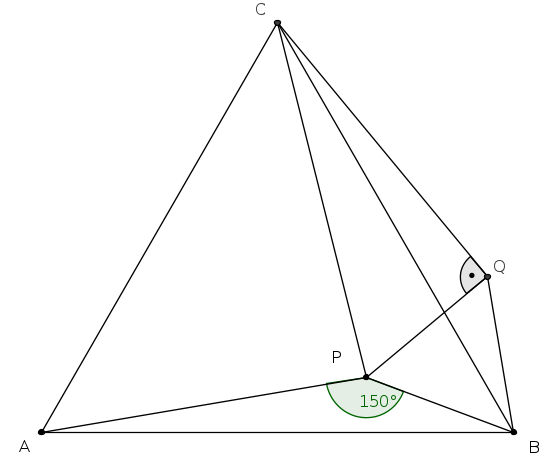
Az \(\displaystyle APB\) háromszöget forgassuk el a \(\displaystyle B\) pont körül \(\displaystyle -60^{\circ}\)-kal. Ekkor az \(\displaystyle A\), \(\displaystyle P\) és \(\displaystyle B\) pont képe rendre \(\displaystyle C=A'\), \(\displaystyle Q=P'\) és \(\displaystyle B=B'\). A forgatás távolság- és szögtartása miatt \(\displaystyle BQ=B'P'=BP\), és \(\displaystyle CQB \sphericalangle = A'P'B' \sphericalangle = APB \sphericalangle = 150^{\circ}\). Továbbá, mivel \(\displaystyle 60^{\circ}\)-kal forgattunk, \(\displaystyle PBQ \sphericalangle = PBP' \sphericalangle = 60^{\circ}\). Azaz a \(\displaystyle PBQ\) háromszög egyenlő szárú és \(\displaystyle 60^{\circ}\)-os szögű, vagyis szabályos. Emiatt \(\displaystyle PQC \sphericalangle = 150^{\circ} - 60^{\circ} = 90^{\circ}\), azaz a \(\displaystyle PQC\) háromszög derékszögű, és így teljesül rá Pitagorasz tétele, \(\displaystyle QC^2 + PQ^2=PC^2\). De a korábbiak alapján \(\displaystyle PQ=PB\) és \(\displaystyle QC=P'A'=PA\), ezeket a fenti Pitagorasz-egyenlőségbe helyettesítve pedig pont \(\displaystyle PA^2+ PB^2 = PC^2\) adódik. Ezzel az állítást igazoltuk.

2. megoldás. Használjuk az alábbi ábrát és jelöléseit!

Az általánosság megszorítása nélkül legyen az \(\displaystyle ABC\) háromszög oldala egységnyi hosszú. Tükrözzük a \(\displaystyle C\) és a \(\displaystyle P\) pontokat az \(\displaystyle AB\) szakasz \(\displaystyle F\) felezőpontjára. Ekkor a \(\displaystyle C\) pont \(\displaystyle C'\) képe az \(\displaystyle APB\) köréírt körének a középpontja, hiszen \(\displaystyle APB \sphericalangle = 150^{\circ}\) miatt \(\displaystyle APB\) körén a rövidebb \(\displaystyle AB\) ívhez \(\displaystyle 30^{\circ}\)-os kerületi szög, és így \(\displaystyle 60^{\circ}\)-os középponti szög tartozik. De ekkor \(\displaystyle C'P=C'A=CA=1\), valamint \(\displaystyle CC'=2CF = 2 \cdot \sqrt{3}/2 = \sqrt{3}\) (az \(\displaystyle ABC\) szabályos háromszög magasságának a duplája).

Továbbá az \(\displaystyle APBP'\) és \(\displaystyle CPC'P'\) négyszögek paralelogrammák (hiszen középpontosan szimmetrikusak), így felírva külön-külön a paralellogrammatételt rájuk:

\(\displaystyle 2 AP^2 + 2 BP^2 = AB^2+PP'^2\), majd \(\displaystyle 2 AP^2 + 2 BP^2 = 1+PP'^2\), illetve \(\displaystyle 2 CP^2 + 2 C'P^2 = CC'^2 + PP'^2\), innen \(\displaystyle 2 CP^2 + 2 = 3 + PP'^2\) és így \(\displaystyle 2 CP^2=1 + PP'^2\) adódik. Mivel mind \(\displaystyle 2 CP^2\), mind a \(\displaystyle 2 AP^2 + 2 BP^2\) összeg is \(\displaystyle 1 + PP'^2\)-tel egyenlő, ezért egymással is egyenlőek, azaz (2-vel osztva) \(\displaystyle AP^2 + BP^2 = CP^2\). Ezzel az állítást igazoltuk.

Statisztika:

102 dolgozat érkezett.
4 pontot kapott:	66 versenyző.
3 pontot kapott:	14 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	6 dolgozat.

A KöMaL 2024. februári matematika feladatai