 |
A B. 5379. feladat (2024. március) |
B. 5379. Az \(\displaystyle ABC\) háromszög \(\displaystyle C\) csúcsánál derékszög van. A \(\displaystyle C\)-ből induló magasságvonal és szögfelező talppontja az \(\displaystyle AB\) átfogón \(\displaystyle H\), illetve \(\displaystyle D\). Az \(\displaystyle AHC\) szög felezője az \(\displaystyle AC\) oldalt az \(\displaystyle E\), a \(\displaystyle CHB\) szög szögfelezője pedig a \(\displaystyle BC\) oldalt az \(\displaystyle F\) pontban metszi. Jelöljük ki a \(\displaystyle HE\) szakaszon az \(\displaystyle M\), a \(\displaystyle HF\) szakaszon pedig az \(\displaystyle N\) pontot úgy, hogy \(\displaystyle HM: HE= HN : HF\) teljesüljön. Mutassuk meg, hogy a \(\displaystyle CD\), \(\displaystyle AM\) és \(\displaystyle BN\) egyenesek egy ponton mennek át.
Javasolta: Nguyen Duy Khanh (Vietnám)
(5 pont)
A beküldési határidő 2024. április 10-én LEJÁRT.
Megoldás. Legyen \(\displaystyle P=AM\cap BN\), és jelölje \(\displaystyle d(X,YZ)\) az \(\displaystyle X\) pont és az \(\displaystyle YZ\) egyenes (előjeles) távolságát; azt kell igazolni, hogy \(\displaystyle P\) rajta van az \(\displaystyle ACB\) szögfelezőjén, vagyis \(\displaystyle d(P,BC)=d(P,CA)\).
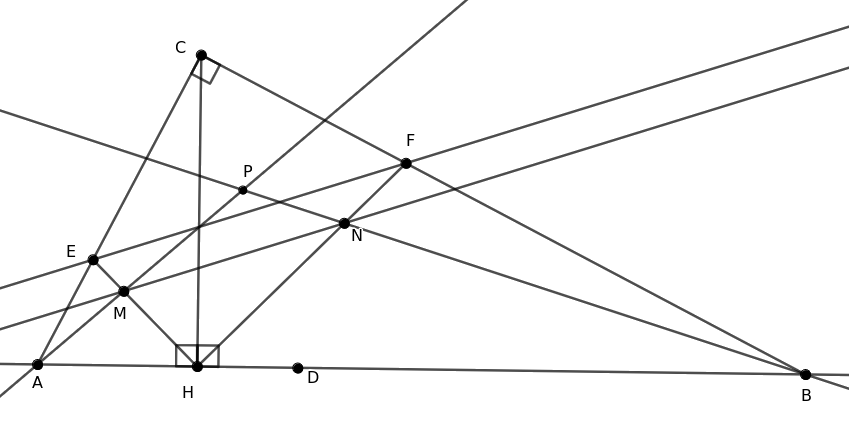
Legyen \(\displaystyle x=\dfrac{ME}{HE}=\dfrac{HN}{HF}\), ekkor
$$\begin{gather*} \dfrac{d(P,AC)}{d(P,AB)} = \dfrac{d(M,AC)}{d(M,AB)} = \dfrac{d(M,AC)}{d(M,HC)} = \dfrac{x\cdot d(H,AC)}{(1-x)\cdot d(E,HC)} = \dfrac{x}{1-x}\cdot\dfrac{d(H,AC)}{d(E,HC)}. \end{gather*}$$Az első egyenlőségnél azt használtuk ki, hogy az \(\displaystyle A\), \(\displaystyle M\) és \(\displaystyle P\) pontok kollineárisak; a másodiknál, hogy \(\displaystyle MH\) felezi a \(\displaystyle CHA\) szöget; a harmadiknál pedig a párhuzamos szelőszakaszok tételét alkalmaztuk kétszer. Hasonlóan, de a második lépést kihagyva láthatjuk be, hogy
\(\displaystyle \dfrac{d(P,BC)}{d(P,AB)}=\dfrac{d(N,BC)}{d(N,AB)}=\dfrac{x\cdot d(H,BC)}{(1-x)\cdot d(F,AB)}=\dfrac{x}{1-x}\cdot\dfrac{d(H,BC)}{d(F,AB)}.\)
Végül vegyük észre, hogy az a \(\displaystyle H\) körüli forgatva nyújtás, ami a \(\displaystyle BCH\) háromszöget a \(\displaystyle CAH\) háromszögbe viszi, egyúttal \(\displaystyle E\)-t \(\displaystyle F\)-be viszi. Mivel a hasonlóság megtartja a megfelelő szakaszok arányát, így
\(\displaystyle \dfrac{d(H,AC)}{d(E,HC)}=\dfrac{d(H,BC)}{d(F,AB)}.\)
Az eddigiek összevetéséből
\(\displaystyle \dfrac{d(P,AC)}{d(P,AB)}=\dfrac{d(P,BC)}{d(P,AB)}\)
adódik, tehát valóban \(\displaystyle d(P,AC)=d(P,BC)\). Ezzel a bizonyítást befejeztük.
Statisztika:
A B. 5379. feladat értékelése még nem fejeződött be.
A KöMaL 2024. márciusi matematika feladatai

