Problem B. 5468. (May 2025)

B. 5468. Let \(\displaystyle r\) be the inradius of the acute triangle \(\displaystyle ABC\), let \(\displaystyle R\) be the circumradius of the same triangle, and let the inradius of the orthic triangle of the triangle \(\displaystyle ABC\) be \(\displaystyle \varrho\). Prove that \(\displaystyle r \ge \sqrt{R\varrho}\).

Proposed by: Viktor Vígh, Sándorfalva

(6 pont)

Deadline expired on June 10, 2025.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Jelöljük az \(\displaystyle ABC\) háromszög beírt körének középpontját \(\displaystyle I\)-vel, magasságpontját \(\displaystyle M\)-mel, és körülírt körének középpontját \(\displaystyle O\)-val, végül a Feuerbach-körének középpontját \(\displaystyle F\)-fel.

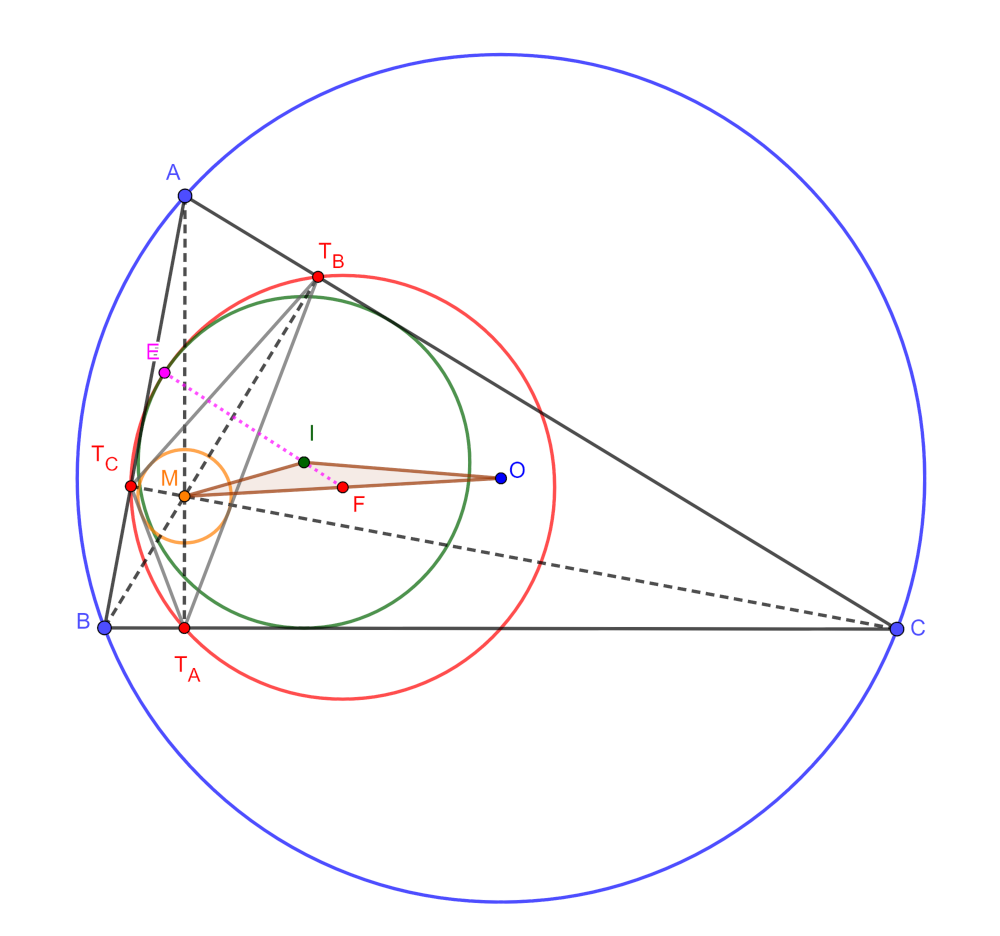
Ismert, hogy \(\displaystyle IM\) felezőpontja \(\displaystyle F\), és használni fogjuk a talpponti háromszög néhány jól ismert tulajdonságát is:

• A talpponti háromszög köréírt köre éppen a Feuerbach-kör, melynek sugara a köréírt kör sugarának fele, azaz a feladat jelöléseivel \(\displaystyle \frac{R}{2}\).
• A talpponti háromszögben a magasságvonalak belső szögfelezők, tehát a talpponti háromszög beírt körének középpontja éppen \(\displaystyle M\).

Tekintsük az \(\displaystyle IMO\) háromszöget az \(\displaystyle IF\) súlyvonalával. Írjuk fel ebben a háromszögben néhány szakasz hosszát.

1. Az Euler-tétel szerint \(\displaystyle IO^2 = R^2-2Rr\).
2. Az Euler-tételt a talpponti háromszögre alkalmazva \(\displaystyle MF^2 = \left(\frac{R}{2} \right)^2 - 2 \frac{R}{2} \varrho = \frac{R^2}{4} - R\varrho\), amiből \(\displaystyle MO^2 = (2MF^2) = R^2 - 4 R \varrho.\)
3. A Feuerbach-tétel szerint a beírt kör belülről érinti a Feuerbach-kört. Az \(\displaystyle E\) érintési pont a két kör \(\displaystyle IF\) centrálisán kell legyen, ezért \(\displaystyle IF = FE - IE = \frac{R}{2}-r\).

Írjuk fel az alábbi (a paralelogramma-tételből vagy Stewart-tételből következő) összefüggést az \(\displaystyle IMO\) háromszög \(\displaystyle IF\) súlyvonalára:

\(\displaystyle 2IM^2+2IO^2 = MO^2 + 4IF^2. \)

Ebből

Tehát \(\displaystyle r^2 - R\varrho = \frac{IM^2}{2} \geq 0\), amivel beláttuk a bizonyítandó állítást. Egyenlőség akkor és csak akkor áll fenn, ha \(\displaystyle I = M\), azaz a háromszög szabályos.

Megjegyzés: Az itt ismertetett megoldás kiolvasható a 2024. októberi B.5413. feladat online is publikált megoldásából.

2. megoldás. Az \(\displaystyle r\) és az \(\displaystyle \varrho\) értékét kifejezzük \(\displaystyle R\)-el és a háromszög szögeivel, és a feladat állítását egy trigonometrikus egyenlőtlenséggé fogalmazzuk át.

Használjuk az ábrán látható betűzést. Az \(\displaystyle IBC\) háromszögben

\(\displaystyle a = BY+YC = 2R\sin\alpha = 4R\sin\frac\alpha2\cos\frac\alpha2 \)

és

\(\displaystyle a = BX+XC = r\ctg\frac\beta2+r\ctg\frac\gamma2 = r \frac{\cos\frac\beta2\sin\frac\gamma2+\sin\frac\beta2\cos\frac\gamma2}{\sin\frac\beta2\sin\frac\gamma2} = r\frac{\sin\frac{\beta+\gamma}2}{\sin\frac\beta2\sin\frac\gamma2} = r\frac{\cos\frac{\alpha}2}{\sin\frac\beta2\sin\frac\gamma2}. \)

Az \(\displaystyle a\) oldal kétféle felírásából azt kapjuk, hogy

\(\displaystyle r = 4R\sin\frac\alpha2\sin\frac\beta2\sin\frac\gamma2. \)

A talpponti háromszög köré írt kör a Feuerbach-kör, sugara \(\displaystyle R/2\). Például az \(\displaystyle ABT_B\), \(\displaystyle AT_AC\) derékszögű háromszögekből és a \(\displaystyle BT_AMT_C\), \(\displaystyle CT_BMT_A\) körökből leolvashatjuk, hogy a talpponti háromszög szögei \(\displaystyle 180^\circ-2\alpha\), \(\displaystyle 180^\circ-2\beta\) és \(\displaystyle 180^\circ-2\gamma\), ezért a fenti okoskodást a talpponti háromszögre megismételve azt kapjuk, hogy

\(\displaystyle \varrho = 4\frac{R}2\sin(90^\circ-\alpha)\sin(90^\circ-\beta)\sin(90^\circ-\gamma)= 2R\cos\alpha\cos\beta\cos\gamma. \)

Ezek után a bizonyítandó állítás azzal ekvivalens, hogy

\(\displaystyle 2\sqrt2 \sin\frac\alpha2\sin\frac\beta2\sin\frac\gamma2 \ge \sqrt{ \cos\alpha\cos\beta\cos\gamma}. \)

Négyzetre emelve és a \(\displaystyle 2\sin^2x=1-\cos 2x\) azonosságot alkalmazva,

\(\displaystyle (1-\cos\alpha)(1-\cos\beta)(1-\cos\gamma) \ge\cos\alpha\cos\beta\cos\gamma, \)

avagy

\(\displaystyle \bigg(\frac{1}{\cos\alpha}-1\bigg) \bigg(\frac{1}{\cos\beta}-1\bigg) \bigg(\frac{1}{\cos\gamma}-1\bigg) \ge 1. \)

Tehát, a feladat megoldásához elég ezt az egyenlőtlenséget igazolnunk.

Legyen \(\displaystyle x=b^2+c^2-a^2\), \(\displaystyle y=c^2+a^2-b^2\) és \(\displaystyle z=a^2+b^2-c^2\). Mivel a háromszög hegyesszögű \(\displaystyle x,y,z>0\). A koszinusztételből

\(\displaystyle \frac{1}{\cos\alpha} = \frac{2bc}{b^2+c^2-a^2} = \frac{\sqrt{2c^2\cdot 2b^2}}{x} = \frac{\sqrt{(x+y)(x+z)}}{x}. \)

A Cauchy–Schwarz egyenlőtlenséget alkalmazva a \(\displaystyle \big(\sqrt{x},\sqrt{y}\big)\) és \(\displaystyle \big(\sqrt{x},\sqrt{z}\big)\) párokra,

\(\displaystyle \sqrt{(x+y)(x+z)} \ge x+\sqrt{yz}, \)

és egyenlőség akkor áll, ha \(\displaystyle \sqrt{x}:\sqrt{y}=\sqrt{x}:\sqrt{z}\), vagyis \(\displaystyle y=z\). Így

\(\displaystyle \frac1{\cos\alpha}-1 \ge \frac{x+\sqrt{yz}}{x}-1 = \frac{\sqrt{yz}}{x}. \)

Ha ezt a másik két szögre is felírjuk, azt kapjuk, hogy

\(\displaystyle \bigg(\frac{1}{\cos\alpha}-1\bigg) \bigg(\frac{1}{\cos\beta}-1\bigg) \bigg(\frac{1}{\cos\gamma}-1\bigg)\ \ge \frac{\sqrt{yz}}{x}\cdot\frac{\sqrt{zx}}{y}\cdot\frac{\sqrt{xy}}{z} = 1, \)

és egyenlőség csak \(\displaystyle x=y=z\), vagyis \(\displaystyle a=b=c\) esetén áll fenn.

Statistics:

23 students sent a solution.
6 points:	Ali Richárd, Aravin Peter, Bencze Mátyás, Bodor Ádám, Bolla Donát Andor, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Holló Martin, Li Mingdao, Rajtik Sándor Barnabás, Sajter Klaus, Sha Jingyuan, Sütő Áron, Vigh 279 Zalán, Wágner Márton, Zhai Yu Fan.
3 points:	3 students.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, May 2025