A C. 1066. feladat (2011. február)

C. 1066. Egy ötszög négy belső szöge 120^o-os. Az ezekkel a szögekkel szemközti, egymáshoz csatlakozó négy oldal hossza sorban: 2, 8, 5, 5. Milyen hosszú az ötödik oldal?

(5 pont)

A beküldési határidő 2011. március 10-én LEJÁRT.

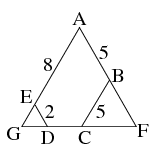
Megoldás. Az ötszög $\displaystyle 120^\circ$-os szögeinek külső szöge $\displaystyle 60^\circ$. Az ötszög ötödik belső szöge $\displaystyle 3\cdot 180^\circ - 4\cdot 120^\circ = 60^\circ$. Az ötszög ezen szöghöz tartozó csúcsa legyen $\displaystyle A$ (a többi sorban $\displaystyle B$, $\displaystyle C$, $\displaystyle D$ és $\displaystyle E$). Az $\displaystyle AB$, $\displaystyle CD$, $\displaystyle EA$ egyenesek meghatározzák az $\displaystyle AFG$ szabályos háromszöget, mert $\displaystyle BFC$ és $\displaystyle DGE$ háromszögek szabályosak. Az általánosság csorbítása nélkül feltehetjük, hogy az egymáshoz csatlakozó négy oldal, melyek $\displaystyle B$, $\displaystyle C$, $\displaystyle D$, $\displaystyle E$ oldalakkal szemközt vannak $\displaystyle DE=2$, $\displaystyle EA=8$, $\displaystyle AB=5$ és $\displaystyle BC=5$. Ekkor $\displaystyle DG=GE=2$ és $\displaystyle BF=FC=5$, továbbá $\displaystyle BC=a$ jelöléssel $\displaystyle AF=AG=10=FG=7+a$, ahonnan $\displaystyle a=3$. A 2, 8, 5, 5 hosszú oldalak más elrendezése nem lehetséges, mert különben $\displaystyle AF\ne AG$. Az ötszög ötödik oldala 3 egység hosszú.

Statisztika:

177 dolgozat érkezett.
5 pontot kapott:	90 versenyző.
4 pontot kapott:	48 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	15 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2011. februári matematika feladatai