A C. 1068. feladat (2011. február)

C. 1068. Egy céltábla 18 mezőjét három koncentrikus kör és a középponton átmenő három szakasz határolja az ábra szerint. Az azonos számmal jelölt mezők területe megegyezik, a 2-es területe fele a 3-asnak. Hányszorosa a 4-es mező területe az 1-esnek?

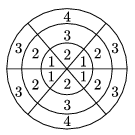
(5 pont)

A beküldési határidő 2011. március 10-én LEJÁRT.

Megoldás. A körök sugara legyen \(\displaystyle \varrho < r < R\) az 1. körcikk szöge (ívmértékben) \(\displaystyle \alpha\). A területek: \(\displaystyle t_1=1/2\alpha\varrho^2\), \(\displaystyle t_2=1/2(\pi - 2\alpha)\varrho^2=1/2\alpha(r^2 - \varrho^2)\), \(\displaystyle t_3=1/2 \alpha(R^2-r^2)=1/2(\pi - 2\alpha)(r^2 - \varrho^2)\), ahonnan \(\displaystyle R^2=\frac{\pi - 2\alpha}{\alpha}(r^2-\varrho^2)+r^2=\). Mivel \(\displaystyle 2t_2=t_3\), ezért -a középső körgyűrűbeli részek összehasonlításából- \(\displaystyle \pi -2\alpha=\alpha\) (azaz \(\displaystyle \alpha=\frac\pi3\)). Végül \(\displaystyle t_4=1/2(\pi - 2\alpha)(R^2-r^2)= 1/2\frac{(\pi - 2\alpha)^2}{\alpha}(r^2 - \varrho^2)=1/2\frac{(\pi - 2\alpha)^3}{\alpha^2}\varrho^2=1/2\frac{8\alpha^3}{\alpha^3}\alpha \varrho^2=8t_1\). A 4-es mező területe nyolcszorosa az 1-es mező területének.

Statisztika:

191 dolgozat érkezett.
5 pontot kapott:	103 versenyző.
4 pontot kapott:	36 versenyző.
3 pontot kapott:	26 versenyző.
2 pontot kapott:	14 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2011. februári matematika feladatai