 |
A C. 1069. feladat (2011. február) |
C. 1069. Négyzetekből készült a következő ábrasorozat, melynek az első három elemét lerajzoltuk:
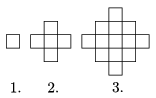
Szakkörön azt a feladatot kapták a tanulók, hogy a sorszám függvényében adják meg az ábrákon látható négyzetek számát. A következő ötletek születtek:
a) ,
b) 1+(n-1).4,
c) 1+(1+2+...+(n-1)).4,
d) (n-1)2+n2.
Melyik ötlet ad jó eredményt?
(5 pont)
A beküldési határidő 2011. március 10-én LEJÁRT.
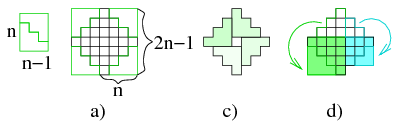
Megoldás. Az a) ötlete lehet az, hogy (az ábra szerint) egy (2n-1)x(2n-1)-es négyzetrácsból vágjuk ki a "sarkokat", ami szerint \(\displaystyle (2n-1)^2-4\cdot\frac{n(n-1)}{2}\) adja az egységnégyzetek számát. b) ötlet \(\displaystyle n=3\)-ra 9 négyzetet határoz meg, ami nem igaz, ezért b) megoldása rossz. c) ötlete lehet az, hogy négy egybevágó "lépcsőből" építsük fel az alakzatot, melyek a középső, le nem fedett négyzet oldalaira illeszkednek, ami szintén jó megoldás. Végül d) ötlete lehetett egy átdarabolás, aminek eredménye egy \(\displaystyle n\) és egy \(\displaystyle n-1\) oldalú négyzet. Tehát a), c) és d) ötlet is jó eredményt ad.
Statisztika:
197 dolgozat érkezett. 5 pontot kapott: 91 versenyző. 4 pontot kapott: 20 versenyző. 3 pontot kapott: 34 versenyző. 2 pontot kapott: 18 versenyző. 1 pontot kapott: 20 versenyző. 0 pontot kapott: 13 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2011. februári matematika feladatai
