A C. 1102. feladat (2011. december)

C. 1102. Az ABC hegyesszögű háromszög C-ből induló magasságának talppontja D. Szerkesszük meg azt az AB-vel párhuzamos egyenest, aminek a háromszögbe eső szakasza D-ből derékszög alatt látszik.

Javasolta: Holló Gábor (Budapest)

(5 pont)

A beküldési határidő 2012. január 10-én LEJÁRT.

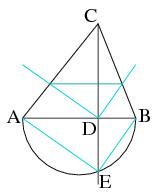
Megoldás. Szerkesszünk \(\displaystyle AB\) fölé Thalesz-kört: a \(\displaystyle C\)-n átmenő magasságegyenest a háromszögön kívül metsze \(\displaystyle E\)-ben. Az \(\displaystyle EAB\) háromszöget középpontosan kicsinyítsük le \(\displaystyle C\)-ből úgy, hogy \(\displaystyle E\) képe \(\displaystyle D\) legyen, azaz \(\displaystyle D\)-n keresztül szerkesszünk párhuzamost \(\displaystyle AE\) és \(\displaystyle BE\) szakaszok egyenesével. Ezen párhuzamosok metszéspontját rendre \(\displaystyle AC\)-vel és \(\displaystyle BC\)-vel összekötve kapjuk azt az \(\displaystyle AB\)-vel párhuzamos szakaszt, mely \(\displaystyle D\)-ből derékszög alatt látszik.

Mivel \(\displaystyle ABC\) hegyesszögű, ezért \(\displaystyle D\) az \(\displaystyle AB\) belsejébe esik, a szerkesztett metszéspontok egyértelműen (és mindig) léteznek.

Statisztika:

191 dolgozat érkezett.
5 pontot kapott:	73 versenyző.
4 pontot kapott:	56 versenyző.
3 pontot kapott:	24 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	25 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2011. decemberi matematika feladatai