Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 1131. feladat (2012. szeptember)

C. 1131. Igazoljuk, hogy ha az ABCD konvex négyszögben AB\parallel CD, továbbá A-nál és B-nél hegyesszög van, akkor

AC2+BD2=AD2+BC2+2.AB.CD.

(5 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. Készítsünk ábrát. Legyen a D-ből, illetve C-ből az AB oldalra állított merőleges talppontja rendre TD és TC.

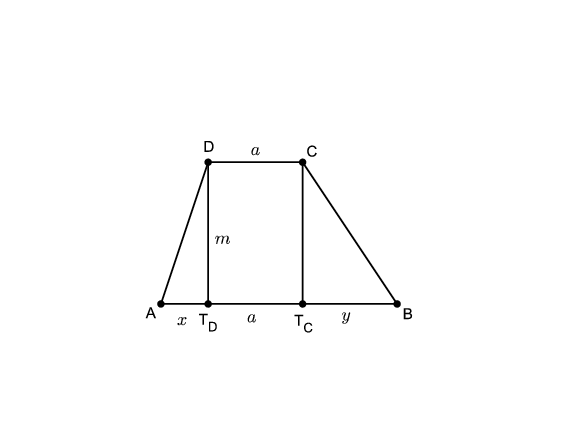
Írjuk fel a Pitagorasz-tételt az ADTD, a BCTC, az ACTC, végül a BDTD derékszögű háromszögekre:

AD2=x2+m2,

BC2=y2+m2,

AC2=m2+(x+a)2,

BD2=m2+(a+y)2.

Ezeket, valamint AB=(x+a+y)-t és CD=a-t behelyettesítve a bizonyítandó állítás a következőképpen néz ki:

m2+(x+a)2+m2+(a+y)2=x2+m2+y2+m2+2.(x+a+y).a.

Ez pedig azonosság.

Statisztika:

369 dolgozat érkezett.
5 pontot kapott:362 versenyző.
4 pontot kapott:3 versenyző.
2 pontot kapott:2 versenyző.
1 pontot kapott:1 versenyző.
0 pontot kapott:1 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai