A C. 1134. feladat (2012. szeptember)

C. 1134. Egy egyenlő szárú trapéz egyik alapja háromszor, a másik kétszer akkora, mint a trapéz magassága. A trapézt az egyik szárával párhuzamos egyenessel egy paralelogrammára és egy egyenlő szárú háromszögre bontjuk, majd megrajzoljuk a trapéz és a paralelogramma átlóit. Bizonyítsuk be, hogy az átlók által határolt háromszög területe a trapéz területének 25-öd része.

(5 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. Jelölje a trapéz magasságát m. Használjuk az ábra jelöléseit.

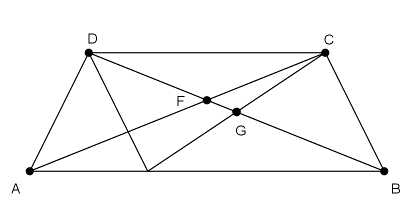
A trapéz területe $\frac{(2m+3m)\cdot m}{2}=\frac{5m^2}{2}$ .

t_FGC=t_DCG-t_DCF.

A paralelogramma átlói felezik egymást, ezért a DCG háromszög magassága m/2:

$t_{DCG}=\frac{2m\cdot\frac m2}{2}=\frac{m^2}{2}.$

A DCF és az ABF háromszögek hasonlók, a hasonlósági arány pedig 2:3. Így a magasságaik aránya is 2:3, vagyis a DCF háromszög magassága $\frac25m$ .

Így

$t_{DCF}=\frac{2m\cdot\frac25m}{2}=\frac25m^2.$

Tehát

$t_{FGC}=\frac{m^2}{2}-\frac25m^2=\frac{m^2}{10}=\frac{1}{25}\cdot\frac{5m^2}{2}.$

Megjegyzés. A feladat állítása igaz, ha az egyik alap 3/2-szerese a másik alapnak, és a magasság tetszőleges.

Statisztika:

318 dolgozat érkezett.

5 pontot kapott: 252 versenyző.

4 pontot kapott: 41 versenyző.

3 pontot kapott: 10 versenyző.

1 pontot kapott: 9 versenyző.

0 pontot kapott: 4 versenyző.

Nem versenyszerű: 2 dolgozat.

A KöMaL 2012. szeptemberi matematika feladatai

318 dolgozat érkezett.
5 pontot kapott:	252 versenyző.
4 pontot kapott:	41 versenyző.
3 pontot kapott:	10 versenyző.
1 pontot kapott:	9 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	2 dolgozat.

Már regisztráltál?
Új vendég vagy?