 |
A C. 1156. feladat (2013. február) |
C. 1156. Egy hold alakú, tengelyesen szimmetrikus medál vázlata az ábrán látható. A holdat határoló félkör sugara 20 mm, a másik határoló körív sugara pedig 25 mm. Határozzuk meg a satírozással jelölt körök sugarát.
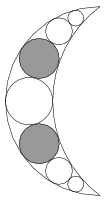
(5 pont)
A beküldési határidő 2013. március 11-én LEJÁRT.
Megoldás. Tekintsük az alábbi ábrát. Legyen 1 egység 5 mm, mert úgy egyszerűbb lesz a számolás.
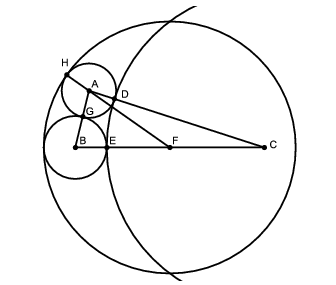
A feladat az \(\displaystyle A\) középpontú kör \(\displaystyle r\) sugarát kérdezi. Mivel \(\displaystyle D\) az \(\displaystyle A\) és a \(\displaystyle C\) sugarú körök érintési pontja, azért \(\displaystyle AD=r\) és \(\displaystyle DC=5\). Mivel \(\displaystyle E\) a \(\displaystyle B\) és a \(\displaystyle C\) középpontú körök érintési pontja, azért \(\displaystyle BE=1\) és \(\displaystyle EF=4-2\cdot1=2\). Innen \(\displaystyle FC=EC-2=5-2=3\). Végül \(\displaystyle H\) az \(\displaystyle A\) és az \(\displaystyle F\) középpontú körök érintési pontja, azért \(\displaystyle HA=r\) és így \(\displaystyle AF=HF-r=4-r\).
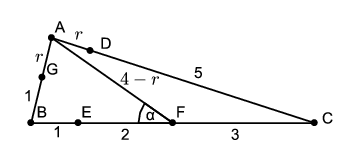
Írjuk fel a koszinusztételt az \(\displaystyle ABF\) háromszögre, majd fejezzük ki \(\displaystyle \cos\alpha\)-t:
\(\displaystyle (1+r)^2=(4-r)^2+3^2-2\cdot(4-r)\cdot3\cos\alpha,\)
| (1) | \(\displaystyle \cos\alpha=\frac{(4-r)^2+3^2-(1+r)^2}{6(4-r)}.\) |
Írjuk fel a koszinusztételt az \(\displaystyle AFC\) háromszögre:
\(\displaystyle (5+r)^2=(4-r)^2+3^2+2\cdot(4-r)\cdot3\cos\alpha.\)
Ebből is kifejezhető \(\displaystyle \cos\alpha\):
| (2) | \(\displaystyle \cos\alpha=\frac{(5+r)^2-(4-r)^2-9}{6(4-r)}.\) |
Mivel (1) és (2) bal oldala megegyezik, ezért jobb oldaluk is egyenlő. Ezt felírva, majd az egyenletet rendezve:
\(\displaystyle \frac{(4-r)^2+3^2-(1+r)^2}{6(4-r)}=\frac{(5+r)^2-(4-r)^2-9}{6(4-r)},\)
\(\displaystyle 16+r^2-8r+9-1-r^2-2r=25+r^2+10r-16-r^2+8r-9,\)
\(\displaystyle 24=28r,\)
\(\displaystyle r=\frac{24}{28}=\frac67.\)
Mivel 1 egység 5 mm, így a kérdéses kör sugara \(\displaystyle \frac{30}{7}\) mm.
Statisztika:
104 dolgozat érkezett. 5 pontot kapott: 58 versenyző. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 13 versenyző. 0 pontot kapott: 9 versenyző.
A KöMaL 2013. februári matematika feladatai
