Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 1162. feladat (2013. március)

C. 1162. Az ABCD paralelogramma rövidebb AC=a átlója, mint átmérő fölé kört írunk. A kör és a paralelogramma metszéspontjai meghatározzák az AIJCKL hatszöget, melynek oldalai rendre \frac a2, b, b, \frac a2, b, b hosszúak. Mekkorák a paralelogramma oldalai és szögei?

(5 pont)

A beküldési határidő 2013. április 10-én LEJÁRT.

Megoldás. Ha a \(\displaystyle CAB\angle\) legalább \(\displaystyle 90^{\circ}\)-os, akkor nem keletkezik hatszög.

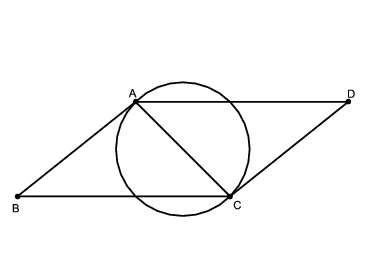
Tehát a \(\displaystyle CAB\angle\) hegyesszög, és így az \(\displaystyle ABC\) háromszög minden szöge az.

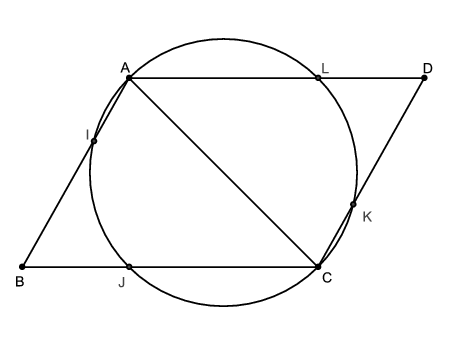
Tudjuk, hogy \(\displaystyle AI=CK=a/2\) és \(\displaystyle IJ=JC=KL=LA=a/2\). Mivel a kör átmérője \(\displaystyle a\), ezért az \(\displaystyle a/2\) hosszú szakaszokhoz \(\displaystyle 60^{\circ}\)-os középponti szög tartozik. Mivel a \(\displaystyle CK\), \(\displaystyle KL\) és \(\displaystyle LA\) szakaszokhoz tartozó középponti szögek összege \(\displaystyle 180^{\circ}\), ezért a \(\displaystyle CK\) szakasznak is \(\displaystyle 60^{\circ}\)-os a középponti szöge. Ebből az is következik, hogy \(\displaystyle CK=KL\), vagyis \(\displaystyle b=a/2\).

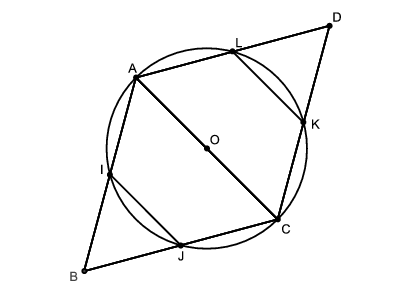
Ezek szerint az \(\displaystyle AOL\), \(\displaystyle LOK\) és \(\displaystyle KOC\) háromszögek szabályosak, így összes szögük \(\displaystyle 60^{\circ}\), és így \(\displaystyle OAL\angle=OCK\angle=60^{\circ}\). Az \(\displaystyle ACD\) háromszög \(\displaystyle A\) és \(\displaystyle C\) csúcsánál levő szögek tehát \(\displaystyle 60^{\circ}\)-osak, vagyis az \(\displaystyle ACD\) háromszög szabályos, \(\displaystyle ADC\angle=60^{\circ}\) és \(\displaystyle AD=DC=AC=a\). A középpontos szimmetria miatt így a paralelogramma szögeinek mérete \(\displaystyle 60^{\circ}\), illetve \(\displaystyle 120^{\circ}\) és minden oldalának hossza \(\displaystyle a\).

Statisztika:

155 dolgozat érkezett.
5 pontot kapott:108 versenyző.
4 pontot kapott:21 versenyző.
3 pontot kapott:15 versenyző.
2 pontot kapott:2 versenyző.
1 pontot kapott:5 versenyző.
0 pontot kapott:4 versenyző.

A KöMaL 2013. márciusi matematika feladatai