 |
A C. 1211. feladat (2014. február) |
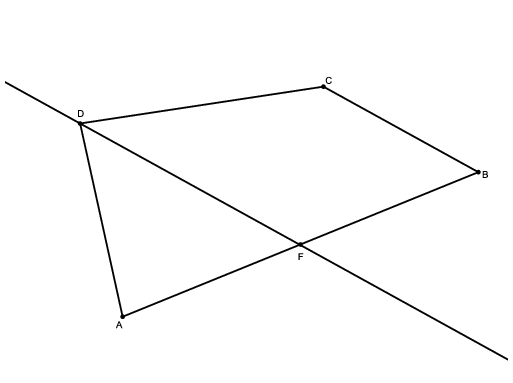
C. 1211. Az ABCD konvex négyszögben a D csúcsra illeszkedő, BC egyenessel párhuzamos egyenes az AB oldalt az oldal F felezőpontjában metszi. Mekkora az AFCD négyszög területe, ha az ABD háromszög területe 4?
(5 pont)
A beküldési határidő 2014. március 10-én LEJÁRT.
Megoldás. Az \(\displaystyle AFCD\) négyszögnek és az \(\displaystyle ABD\) háromszögnek is része az \(\displaystyle AFD\) háromszög. Ennek területéhez adjuk hozzá a \(\displaystyle DFC\), illetve a \(\displaystyle DFB\) háromszög területét. E két háromszögnek közös a \(\displaystyle DF\) oldala, valamint a \(\displaystyle DF\)-hez tartozó magasságuk is azonos hosszúságú, hiszen \(\displaystyle DF\) párhuzamos \(\displaystyle CB\)-vel. Így területük megegyezik. Tehát az \(\displaystyle AFCD\) négyszög területe egyenlő az \(\displaystyle ABD\) háromszög területével, vagyis 4.
Statisztika:
121 dolgozat érkezett. 5 pontot kapott: 91 versenyző. 4 pontot kapott: 6 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 9 dolgozat.
A KöMaL 2014. februári matematika feladatai
