A C. 1227. feladat (2014. április)

C. 1227. Egy trapéz alapjainak hossza 7, illetve 1. Az alapokkal párhuzamos egyenessel két egyenlő területű részre vágtuk a trapézt. Mekkora darabja esik az egyenesnek a trapéz belsejébe?

(5 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldás. Legyen az $\displaystyle ABCD$ trapézban $\displaystyle CD=1$, $\displaystyle AB=7$, a keresett egyenesnek a trapézba eső szakasza $\displaystyle MN$, hossza $\displaystyle x$. Az $\displaystyle AD$ és $\displaystyle BC$ egyenes metszéspontját jelölje $\displaystyle O$. Az $\displaystyle ODC$, az $\displaystyle OMN$ és az $\displaystyle OAB$ háromszög magassága legyen rendre $\displaystyle m$, $\displaystyle m_1$ és $\displaystyle m_2$.

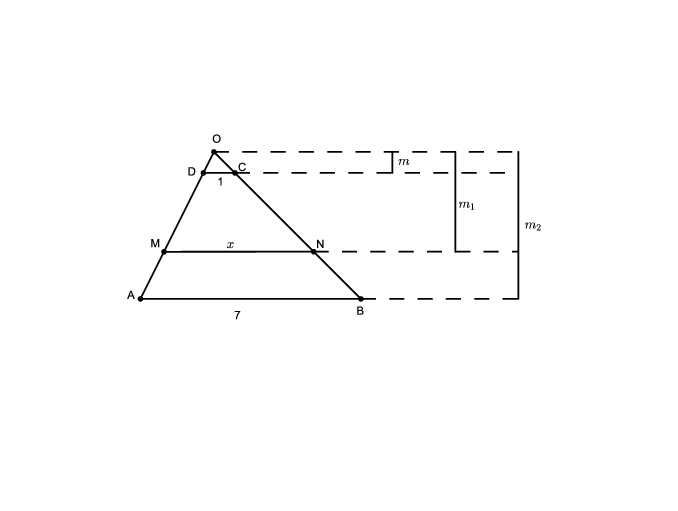
$\displaystyle DC||MN$, így az $\displaystyle ODC$ és az $\displaystyle OMN$ háromszögek hasonlók, így megfelelő szakaszaik aránya megegyezik: $\displaystyle \frac 1x=\frac{m}{m_1}$, amiből $\displaystyle m_1=mx$.

Ugyanígy az $\displaystyle ODC$ és az $\displaystyle OAB$ háromszögek is hasonlóak, és így $\displaystyle \frac17=\frac{m}{m_2}$, amiből $\displaystyle m_2=7m$.

A $\displaystyle DMNC$ trapéz magassága $\displaystyle m_1-m=mx-m=m(x-1)$, míg az $\displaystyle ABCD$ trapéz magassága $\displaystyle m_2-m=7m-m=6m$. Az előbbi területe fele az utóbbinak:

$\displaystyle 2\cdot\frac{(1+x)m(x-1)}{2}=\frac{(1+7)\cdot6m}{2},$

$\displaystyle m>0$-val osztva és rendezve:

$\displaystyle (1+x)(x-1)=24,$

$\displaystyle x^2=25,$

és innen $\displaystyle x>0$ miatt $\displaystyle x=5$ következik.

Statisztika:

114 dolgozat érkezett.
5 pontot kapott:	100 versenyző.
4 pontot kapott:	4 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2014. áprilisi matematika feladatai