A C. 1262. feladat (2014. december)

C. 1262. Bizonyítsuk be, hogy ha egy húrnégyszög egyben érintőnégyszög is, és az egyik szöge derékszög, akkor szimmetrikus.

(5 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldás. Mivel a négyszög húrnégyszög, és egyik szöge derékszög, ezért az azzal szemben lévő szög is az. Használjuk az ábra jelöléseit.

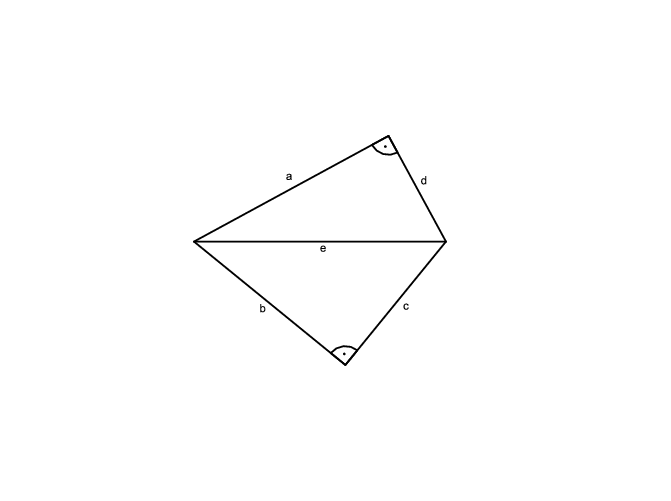
A Pitagorasz-tételt felírva a két derékszögű háromszögre:

$\displaystyle a^2+d^2=e^2=b^2+c^2.$

Mivel a négyszög érintőnégyszög, ezért szemközti oldalainak összege egyenlő:

$\displaystyle a+c=b+d,$

amit négyzetre emelve:

$\displaystyle a^2+c^2+2ac=b^2+d^2+2bd.$

Ebből kivonva az $\displaystyle a^2+d^2=b^2+c^2$ egyenlőséget, kapjuk, hogy

$\displaystyle c^2-d^2+2ac=d^2-c^2+2bd,$

$\displaystyle 2c^2+2ac=2d^2+2bd,$

$\displaystyle 2c(c+a)=2d(d+b).$

Mivel $\displaystyle a+c=b+d\neq0$, oszthatjuk vele mindkét oldalt, így kapjuk, hogy

$\displaystyle 2c=2d,$

vagyis $\displaystyle c=d$, és így $\displaystyle a=b$, vagyis a négyszög az $\displaystyle e$ átlójára szimmetrikus deltoid.

Statisztika:

168 dolgozat érkezett.
5 pontot kapott:	91 versenyző.
4 pontot kapott:	16 versenyző.
3 pontot kapott:	9 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	29 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2014. decemberi matematika feladatai