A C. 1264. feladat (2014. december)

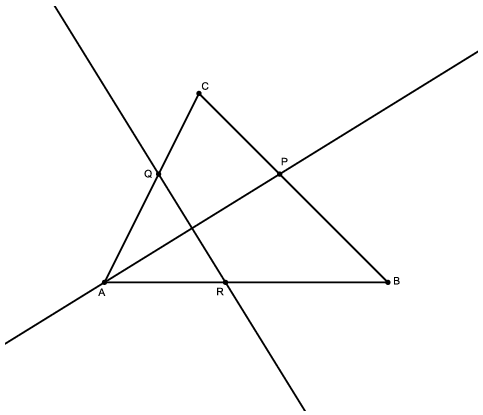
C. 1264. Az \(\displaystyle ABC\) háromszög \(\displaystyle A\) csúcsából induló belső szögfelező a szemközti oldalt a \(\displaystyle P\) pontban, az \(\displaystyle AP\) szakasz felezőmerőlegese az \(\displaystyle AC\) oldalt a \(\displaystyle Q\) pontban metszi. Fejezzük ki az \(\displaystyle ABPQ\) négyszög területét az \(\displaystyle AB\), \(\displaystyle AQ\) szakaszok és a \(\displaystyle BAQ\) szög ismeretében.

(5 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldás. Mivel \(\displaystyle Q\) rajta van az \(\displaystyle AP\) szakasz felező merőlegesén, így az \(\displaystyle AQP\) háromszög egyenlőszárú. Azt is tudjuk, hogy \(\displaystyle AP\) felezi az \(\displaystyle \alpha=CAB\angle\)-et. Ezekből következik, hogy \(\displaystyle APQ\angle = PAQ\angle= BAP\angle\). Tehát az \(\displaystyle APQ\angle\) és a \(\displaystyle BAP\angle\) párhuzamos szárú szögek kell, hogy legyenek, vagyis \(\displaystyle AB||QP\), az \(\displaystyle ABPQ\) négyszög trapéz. Mivel \(\displaystyle QP=AQ\) és \(\displaystyle \sin\alpha=\frac{m}{AQ}\), amiből \(\displaystyle m=AQ\sin\alpha\), így

\(\displaystyle t_{ABPQ}=\frac{(AB+AQ)\cdot AQ\sin\alpha}{2}.\)

Statisztika:

57 dolgozat érkezett.
5 pontot kapott:	52 versenyző.
4 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. decemberi matematika feladatai