A C. 1296. feladat (2015. május)

C. 1296. Mekkorák annak a hegyesszögű egyenlőszárú háromszögnek a szögei, melynek súlypontját az egyik magasság talppontjára tükrözve a tükörkép a háromszög alapjának egyenesére esik?

(5 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. Jelölje a háromszög szárát $\displaystyle a$, súlypontját $\displaystyle S$, az $\displaystyle A$ csúcsból induló magasság talppontját $\displaystyle T$, az $\displaystyle AB$ oldal felezőpontját $\displaystyle F$, az $\displaystyle S$ pont tükörképét a $\displaystyle T$ pontra $\displaystyle S'$, végül az $\displaystyle S$ ponton át az $\displaystyle AB$ alappal húzott párhuzamos és $\displaystyle BC$ metszéspontját $\displaystyle U$.

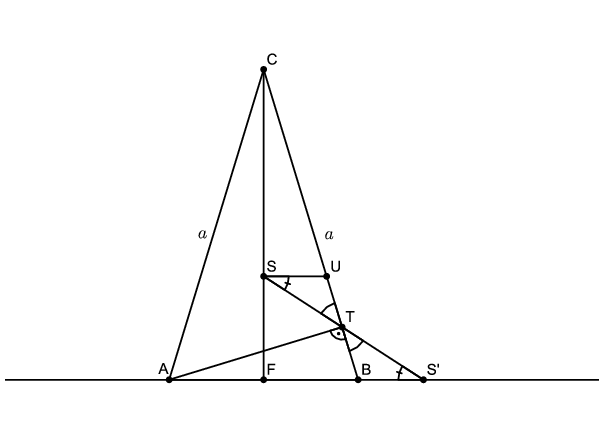
Ekkor $\displaystyle UST\angle=BS'T\angle$, mert párhuzamos szárú szögek; és $\displaystyle UTS\angle=BTS'\angle$, mert csúcsszögek. A tükrözés miatt $\displaystyle ST=S'T$. Tehát $\displaystyle SUT\triangle\cong S'BT\triangle$, mert két szögük és egy megfelelő oldaluk egyenlő. Így a másik két megfelelő oldalban is megegyeznek, vagyis $\displaystyle UT=BT$.

$\displaystyle CSU\triangle\cong CFB\triangle$, hiszen $\displaystyle SU||FB$, a másik két oldalegyenesük pedig egybeesik, és emiatt a szögeik egyenlők. Ebből $\displaystyle \frac{CU}{CB}=\frac{CS}{CF}=\frac23$, amiből $\displaystyle CU=\frac23a$, és így $\displaystyle UB=a-\frac23a=\frac13a$. Mivel $\displaystyle UT$ ennek fele, így $\displaystyle UT=\frac16a$. Ebből pedig $\displaystyle CT=CU+UT=\frac23a+\frac16a=\frac56a$.

Az $\displaystyle ATC$ derékszögű háromszögben $\displaystyle \cos ACB\angle=\cos ACT\angle=\frac{CT}{CA}=\frac{\frac56a}{a}=\frac56$, amiből $\displaystyle ACB\angle=\rm{arccos}\frac56\approx33,56^{\circ}$, és így $\displaystyle BAC\angle=ABC\angle=\frac{180-33,56}{2}\approx 73,22^{\circ}$.

Statisztika:

60 dolgozat érkezett.
5 pontot kapott:	Egyházi Anna, Fehér Balázs, Fekete Balázs Attila, Fényes Balázs, Glasznova Maja, Klász Viktória, Kocsis Júlia, Kormányos Hanna Rebeka, Mihálykó Péter, Souly Alexandra, Szabó Alexandra, Telek Máté László.
4 pontot kapott:	Bereczki Zoltán, Bindics Boldizsár, Csahók Tímea, Csapó Márton, Édes Lili, Erdei Ákos, Farkas Dóra, Fülöp Erik, Horváth Botond, Kasó Ferenc, Knoch Júlia, Kósa Szilárd, Krisztián Jonatán, Mályusz Attila, Mátyus Adrienn, Mikulás Zsófia, Páhoki Tamás, Paróczai György, Sándor Gergely, Schrettner Jakab, Sebastian Fodor, Szalay Bence, Szécsi Adél Lilla, Szepesvári Csongor, Szücs Patrícia, Takács Péter György, Tatai Mihály, Temesvári Bence, Tevesz Judit, Tóth Tamás, Varga-Umbrich Eszter, Vida Máté Gergely.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2015. májusi matematika feladatai