A C. 1298. feladat (2015. május)

C. 1298. A mellékelt ábra egy parkot szemléltet, ahol a szakaszok mutatják az ösvényeket. Hányféleképpen juthatunk el a bejárattól a kijáratig, ha minden ösvényen legfeljebb egyszer mehetünk végig, és az ösvényekről nem térhetünk le?

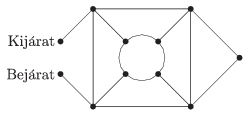
(5 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. Tekintsünk a parkra, mint egy gráfra, a csúcsokat jelöljük az I. rajz szerint. A Bejárattól a C csúcsig, illetve az F csúcstól a Kijáratig mindig vezet él. A Bejáraton és a Kijáraton kívül a többi csúcs foka páros kell, hogy legyen. A továbbiakban az FC, illetve az ED élt vízszintes élnek, a CD és az FE élt pedig függőleges élnek tekintjük.

Három hosszú séta csak egy van, az I. rajzon látható. Öt hosszú két darab van, a II. és a III. rajzon láthatóak. Ha a III. rajzbeli DE élt kicseréljük a DKE két hosszú útra, akkor megkapjuk az egyetlen hat hosszú sétát, mely a IV. rajzon látható.

Általában, egy függőleges vagy egy vízszintes élt ki lehet cserélni egy három hosszú útra, a DE élt két hosszú útra is. (Amennyiben a kérdéses élek még nem foglaltak.)

Hét hosszú séta készítésére az az egyik lehetőség, hogy egy öt hosszú sétában egy élt kicserélünk egy három hosszú útra.

Ha a II. rajzbeli GJ élt kicseréljük a GHIJ élsorozatra, egy hét hosszú sétát kapunk. Ebben a IJF részt kicserélhetjük a IEF részre (VI. rajz), hasonlóan a CGH részt a CDH-ra (VII. rajz).

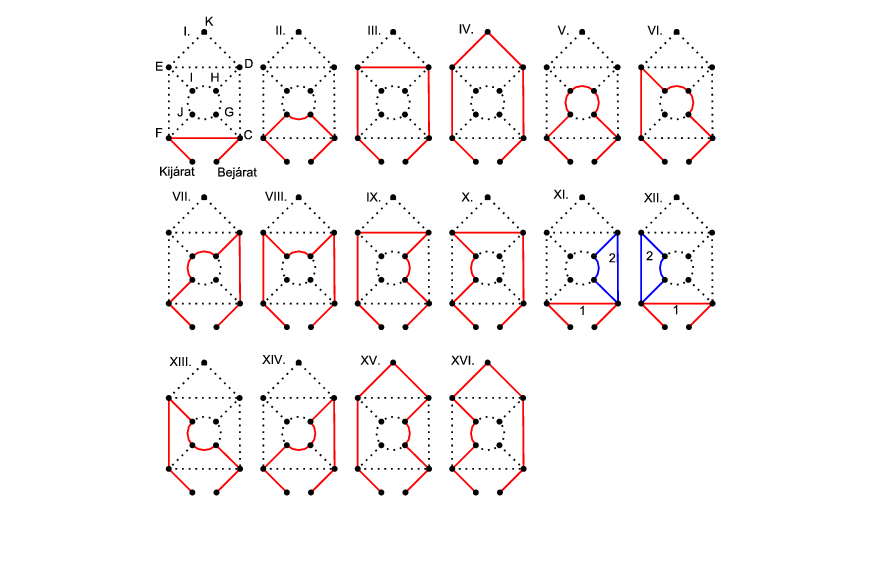
A III. rajzon kicserélhetjük a DE élt DHIE élsorozatra (VIII. rajz), vagy a CD élt a CGHD élsorozatra (IX. rajz), vagy az EF élt az EIJF élsorozatra (X. ábra). A VI. rajzon a GHI élsorozat helyett vehetjük a GJI éleket (XIII. rajz), hasonlóan a VII. rajzon a HIJ élek helyett vehetjük a HGJ éleket (XIV. rajz).

A hat hosszú sétában már benne vannak a DK és a KE élek, így nem tudjuk eggyel megnövelni a hosszát.

A három hosszú sétához négy hosszú köröket tudunk tenni. A XI. rajzon a kék éleket két irányban is bejárhatjuk: CDHGCF vagy CGHDCF; hasonlóan a XII. ábra is két bejárást takar.

Másképp nem kapunk hét hosszú sétát, így abból összesen 12 van.

Nyolc hosszú sétát úgy kapunk, hogy a hat hosszú séta egyik élét kicseréljük egy három hosszú útra, erre két lehetőség van (XV. és XVI. rajz).

A kilenc hosszú sétákat a XVII. rajztól kezdve a XXVII. rajzig bezárólag láthatjuk. Az egyszerűség kedvéért az 1. rajz kivételével a séta kezdő és befejező lépését elhagytuk.

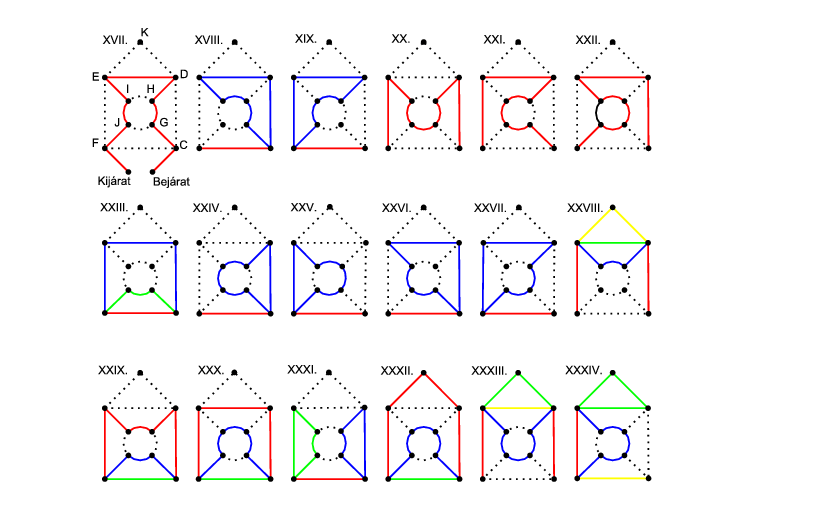
A IX. vagy X. rajzban kicserélhetünk egy függőleges élt egy három hosszú útra (XVII. rajz). A többi kilenc hosszú sétát ábrázoló rajzot a fentiekhez hasonló módon kaptuk: egy rövidebb sétát módosítottunk valahogy, vagy akár a meglévő kilences séta két élét cseréltük le másik kettőre. Ahol csak piros vonal van, ott a bejárás egyértelmű. A XVIII., XIX., XXIV. XXV., XXVI. és XXVII. rajzokon a kék köröket két irányban is bejárhatjuk. A XXIII. rajzon A C csúcsból három irányba mehetünk. Mindhárom esetben az F csúcsot elérve, ott két irányba mehetünk, innen már egyértelmű a befejezés. Tehát ezt a rajzot \(\displaystyle 3\cdot2=6\)-féleképp járhatjuk be.

Vagyis kilenc hosszú séta összesen \(\displaystyle 4+6\cdot2+6=22\) van.

Tíz hosszú sétát kétféleképp kaphatunk. Az egyik, hogy egy DE élt tartalmazó kilenc hosszú sétában a DE élt kicseréljük a DKE három hosszú útra. Erre \(\displaystyle 3+4\cdot2+6=17\) lehetőség van. A másik, hogy egy DE élt nem, de a D vagy az E csúcsot tartalmazó hét hosszú sétához hozzátesszük a DKED/DEKD vagy az EDKE/EKDE kört. Ha az E és D csúcsból pontosan az egyik van benne a hét hosszú sétában, akkor ez az adott séták számának dupláját adja eredményül: \(\displaystyle 4\cdot2+2\cdot2\cdot2=16\). Ha mindkét csúcs benne van, akkor kapjuk a XXVIII. rajzot. Itt a D csúcsból három irányba mehetünk az E csúcsig, ott két irányban visssza a D-be, ahonnan a befejezés már adott. Ez \(\displaystyle 3\cdot2=6\) eset.

Tíz hosszú séta összesen \(\displaystyle 17+16+6=39\) van.

A tizenegy hosszú sétákat a XXIX., XXX. és XXXI. rajzok mutatják. A séták száma: \(\displaystyle 3\cdot2+3\cdot2+2\cdot2=16\). (A XXXI. rajzon nem indulhatunk a piros úton, mert akkor nem jutunk el a kék részhez.)

A tizenkét hosszú sétákat a XXXII., XXXIII. és a XXXIV. rajz mutatja, a XXXIV. rajz "tükörképe" is jó, ahol a másik függőleges él szerepel. A lehetőségek száma: \(\displaystyle 3\cdot2+3\cdot2+2\cdot2+2\cdot2=20\).

Mivel összesen tizenhat él van, és csak négy csúcs foka páratlan, ezért már csak tizennégy hosszú séták lehetségesek. Ekkor a középső köríves részből kell elhagyni két szemközti élt. A lehetőségeket a 3. ábra rajzai mutatják. A Bejárat-C és a Kijárat-F éleket nem véve figyelembe, ahol egy színnel jelöltünk egy élsorozatot, azt mindenképpen megszakítás nélkül tesszük meg a séta során. (Könnyebb összeszámolni, ha így megkülönböztetünk eseteket.) Az első két rajzon a sárga, zöld és fekete éleket bejárhatjuk egymás után úgy is, hogy két különböző színnel kört alkotunk. A többi ábrán a piros-zöld, piros-kék, illetve sárga-fekete, együtt kört alkotó részeket nem egymás után járjuk be.

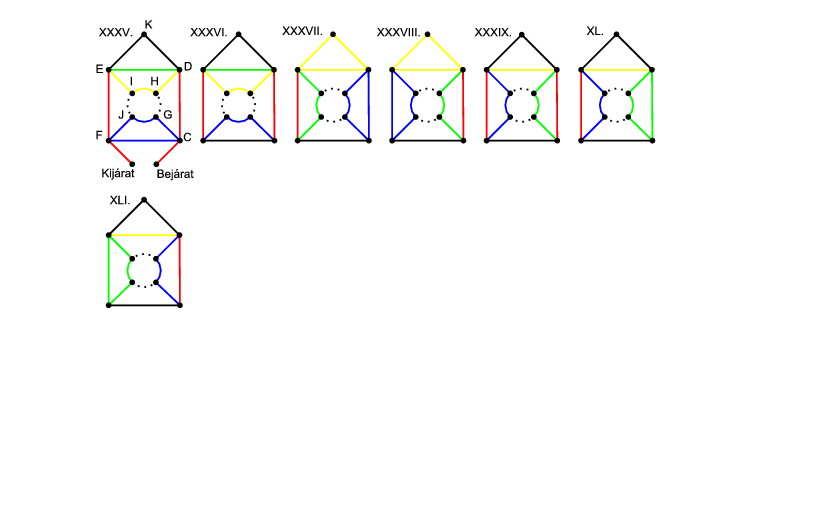
Külön-külön összeszámoljuk, hogy az egyes rajzoknak hány bejárása van. A XXXV. rajzon a C csúcsból mehetünk a D felé, onnan már nem mehetünk vissza a C-be, így \(\displaystyle 3\cdot2=6\) lehetőség van rá, hogy milyen sorrendben járjuk be a sárga, zöld és fekete részt. Az E-ből csak F-be mehetünk, ahonnan a kék részt kétféleképp járhatjuk be. Ez eddig \(\displaystyle 6\cdot2=12\) eset. Ha a kék körrel kezdjük, az szintén 12 lehetőség. Ezt a rajzot tehát \(\displaystyle 2\cdot12=24\)-féle módon járhatjuk be.

A XXXVI. rajzot csak akkor kapjuk, ha a C csúcsból az F felé indulunk, és onnan az E-be megyünk tovább, ott bejárjuk a fekete, zöld és sárga részt, majd a D csúcsból lemegyünk a C-be, és onnan az F-be. Erre összesen \(\displaystyle 2\cdot6=12\) módunk van.

Ha a másik két belső élt hagyjuk ki, akkor a felső háromszöget bejárhatjuk egyben, vagy külön. Ha egyben járjuk be, akkor a XXXVII. vagy a XXXVIII. rajzot kapjuk. A fentikehez hasonló gondolatmenettel a XXXVII. rajz bejárására \(\displaystyle 2\cdot2\cdot2=8\), a XXXVIII. rajzéra \(\displaystyle 2\cdot2\cdot2=8\), a XXXIX. rajzéra \(\displaystyle 2\cdot2\cdot2=8\), a XL. rajzéra \(\displaystyle 2\cdot2\cdot2=8\), végül a XLI. rajzéra \(\displaystyle 2\cdot2\cdot2=8\) lehetőség van.

Tizennégy hosszú séta összesen \(\displaystyle 24+12+8+8+8+8+8=76\) van.

A séták száma összesen \(\displaystyle 1+2+1+12+2+22+39+16+20+76=191\).

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Bindics Boldizsár, Bottlik Judit, Egyházi Anna, Fehér Balázs, Fekete Balázs Attila, Fényes Balázs, Fülöp Erik, Glasznova Maja, Jakus Balázs István, Kasó Ferenc, Klász Viktória, Knoch Júlia, Kocsis Júlia, Kósa Szilárd, Mándoki Sára, Schrettner Jakab, Sebastian Fodor, Souly Alexandra, Tevesz Judit.
4 pontot kapott:	Kormányos Hanna Rebeka, Marton Fruzsina.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. májusi matematika feladatai