A C. 1300. feladat (2015. május)

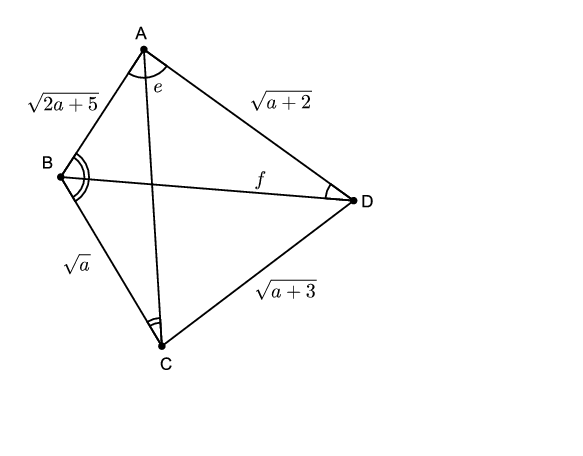
C. 1300. Egy konvex négyszög oldalainak hossza sorban \(\displaystyle \sqrt{a}\), \(\displaystyle \sqrt{a+3}\), \(\displaystyle \sqrt{a+2}\) és \(\displaystyle \sqrt{2a+5}\), mindkét átlója \(\displaystyle \sqrt{2a+5}\) hosszú. Határozzuk meg a négyszög legnagyobb szögét.

(5 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. Készítsünk ábrát. Először megnézzük, hogy az \(\displaystyle ABD\), \(\displaystyle CDB\), \(\displaystyle CDA\) és \(\displaystyle CAB\) háromszögekben a legnagyobb oldallal szemközti szög hegyes-, tompa-, vagy derékszög. Az \(\displaystyle ABD\) háromszögben az oldalak négyzetére \(\displaystyle 2a+5<2a+5+a+2\), tehát \(\displaystyle BAD\angle<90^{\circ}\). A \(\displaystyle CDB\) háromszögben \(\displaystyle 2a+5>a+a+3\), tehát \(\displaystyle BCD\angle>90^{\circ}\). A \(\displaystyle CDA\) háromszögben \(\displaystyle 2a+5=a+2+a+3\), tehát \(\displaystyle CDA\angle=90^{\circ}\). Végül a \(\displaystyle CAB\) háromszögben \(\displaystyle 2a+5<2a+5+a\), tehát \(\displaystyle CBA\angle<90^{\circ}\). A négyszög legnagyobb szöge tehát a \(\displaystyle BCD\angle\).

Az \(\displaystyle ABC\) egyenlő szárú háromszögben \(\displaystyle \cos BCA\angle=\frac{\frac{\sqrt{a}}{2}}{\sqrt{2a+5}}=\sqrt{\frac{a}{8a+20}}\). Ebből a \(\displaystyle \sin^2\alpha+\cos^2\alpha=1\) összefüggés alapján \(\displaystyle \sin BCA\angle=\sqrt{\frac{7a+20}{8a+20}}\).

Az \(\displaystyle ACD\) derékszögű háromszögben \(\displaystyle \sin ACD\angle=\frac{\sqrt{a+2}}{\sqrt{2a+5}}=\sqrt{\frac{a+2}{2a+5}}\) és \(\displaystyle \cos ACD\angle=\frac{\sqrt{a+3}}{\sqrt{2a+5}}=\sqrt{\frac{a+3}{2a+5}}\).

Tehát \(\displaystyle \cos BCD\angle=\cos(BCA\angle+ACD\angle)=\cos BCA\angle\cos ACD\angle-\sin BCA\angle\sin ACD\angle=\sqrt{\frac{a(a+3)}{4(2a+5)^2}}-\sqrt{\frac{(a+2)(7a+20)}{4(2a+5)^2}}\).

A \(\displaystyle BCD\angle\) koszinuszát a \(\displaystyle BCD\) háromszögre felírt koszinusz-tételből is megkaphatjuk:

\(\displaystyle 2a+5=a+a+3-2\sqrt{a(a+3)}\cos BCD\angle,\)

amiből

\(\displaystyle \cos BCD\angle=\frac{-2}{2\sqrt{a(a+3)}}.\)

A \(\displaystyle \cos BCD\) szögre kapott két érték egyenlő:

\(\displaystyle \frac{-2}{2\sqrt{a(a+3)}}=\sqrt{\frac{a(a+3)}{4(2a+5)^2}}-\sqrt{\frac{(a+2)(7a+20)}{4(2a+5)^2}}.\)

Mindkét oldalt szorozva \(\displaystyle 2\sqrt{a(a+3)}\cdot(2a+5)\)-tel:

\(\displaystyle -2(2a+5)=a(a+3)-\sqrt{a(a+2)(a+3)(7a+20)},\)

\(\displaystyle \sqrt{a(7a+20)(a+3)(a+2)}=a^2+7a+10,\)

négyzetre emelve

\(\displaystyle (7a^2+20a)(a^2+5a+6)=(a^2+7a+10)^2,\)

\(\displaystyle 7a^4+55a^3+142a^2+120a=a^4+49a^2+100+14a^3+20a^2+140a,\)

\(\displaystyle 6a^4+41a^3+73a^2-20a-100=0.\)

Könnyen látszik, hogy \(\displaystyle a=1\) megoldás, így \(\displaystyle (a-1)\)-et kiemelve:

\(\displaystyle (a-1)(6a^3+47a^2+120a+100)=0.\)

Mivel most \(\displaystyle a>0\), ezért a második tényező biztosan pozitív, így az egyetlen megoldás az \(\displaystyle a=1\). Ekkor \(\displaystyle \cos BCD\angle=\frac{-2}{2\sqrt{a(a+3)}}=-\frac12\), amiből \(\displaystyle BCD\angle=120^{\circ}\).

Statisztika:

22 dolgozat érkezett.
5 pontot kapott:	Bottlik Judit, Brányi Balázs, Egyházi Anna, Erdei Ákos, Farkas Dóra, Fehér Balázs, Fényes Balázs, Fülöp Erik, Kasó Ferenc, Kósa Szilárd, Krisztián Jonatán, Mándoki Sára, Szücs Patrícia.
4 pontot kapott:	Bereczki Zoltán.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	2 versenyző.

A KöMaL 2015. májusi matematika feladatai