 |
A C. 1383. feladat (2016. november) |
C. 1383. Az \(\displaystyle AB\) szakasz felezőpontja \(\displaystyle O\), az \(\displaystyle A\) ponthoz közelebbi negyedelőpontja \(\displaystyle C\), a \(\displaystyle B\) ponthoz közelebbi negyedelőpontja \(\displaystyle D\). A \(\displaystyle C\), \(\displaystyle O\) és \(\displaystyle D\) pontokban az \(\displaystyle AB\) szakaszra rajzolt merőlegesek az \(\displaystyle AB\) átmérőjű félkört rendre a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) pontokban metszik. Határozzuk meg a \(\displaystyle PQB\) és a \(\displaystyle QRB\) háromszögek szögeit.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2016. december 12-én LEJÁRT.
Megoldás. Az \(\displaystyle AB\) átmérőjű körben a \(\displaystyle BOQ\) középponti szög értéke \(\displaystyle 90^{\circ}\). A kerületi és középponti szögek tétele miatt \(\displaystyle BPQ\) kerületi szög \(\displaystyle 45^{\circ}\). Mivel a \(\displaystyle BPQR\) négyszög húrnégyszög, ezért \(\displaystyle QRB∡=180^{\circ}-45^{\circ}=135^{\circ}\).
\(\displaystyle OB=OR=r\), \(\displaystyle OD=\frac{OB}{2}=\frac r2\), így az \(\displaystyle ODR\) derékszögű háromszögben a rövidebbik befogó az átfogó fele, ezért hegyesszögei: \(\displaystyle DOR∡=60^{\circ}\) és \(\displaystyle DRO∡=30^{\circ}\). \(\displaystyle BOQ\) egyenlő szárú derékszögű háromszög, ezért \(\displaystyle BQO∡=45^{\circ}\).
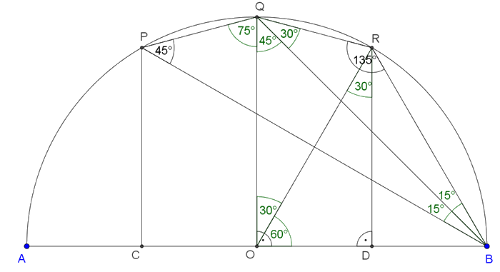
A \(\displaystyle BOR\) középponti szöghöz tartozó kerületi szög \(\displaystyle BQR∡=30^{\circ}\). A szimmetria miatt \(\displaystyle PQO∡=RQO∡=45^{\circ}+30^{\circ}=75^{\circ}\). \(\displaystyle ROQ∡=90^{\circ}-60^{\circ}=30^{\circ}\). Ehhez, mint középponti szöghöz tartozó kerületi szög \(\displaystyle RBQ∡=15^{\circ}\). \(\displaystyle PBQ∡=15^{\circ}\), mert \(\displaystyle RBQ\) szöggel megegyező íven nyugvó kerületi szög a körben.
Ezek alapján \(\displaystyle PQBΔ\) szögei: \(\displaystyle 45^{\circ}\), \(\displaystyle 120^{\circ}\) és \(\displaystyle 15^{\circ}\). A \(\displaystyle QRBΔ\) szögei: \(\displaystyle 30^{\circ}\), \(\displaystyle 135^{\circ}\) és \(\displaystyle 15^{\circ}\).
Statisztika:
80 dolgozat érkezett. 5 pontot kapott: Árvai Balázs, Balbisi Mirjam, Csapó Márton, Dézsi Viktória, Édes Lili, Gera Dóra, Gergály Szabolcs, Jakus Péter János, Kaposi Benedek, Kis 999 Alexandra, Kocsis Júlia, Kormányos Hanna Rebeka, Mácz Andrea, Mészáros Bálint, Mészáros Melinda, Nagy Odett, Nagy Olivér, Németh Csilla Márta, Pap-Takács Noémi, Pszota Máté, Szabadfalvi Dániel, Szalay Gergő, Szécsi Adél Lilla, Szilágyi Éva, Szűcs 865 Eszter, Takács 666 Réka, Tanács Viktória, Tatai Mihály, Török Attila, Varga 157 Kristóf, Veibli-Magyari Kristóf, Zeller Doroti, Zsombó István. 4 pontot kapott: Agócs Katinka, Antal Georgina, Erdélyi Janka, Erdődi Ádám Károly, Gálik Annamária, Horváth 546 János, Karajz Ágnes Fruzsina, Kocsis Ábel, Nagy Enikő, Ondrik Ákos, Perényi Gellért, Radó Albert, Sántha 001 Balázs, Simon Ákos, Surján Anett, Szalay Dorottya. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2016. novemberi matematika feladatai
